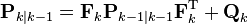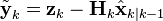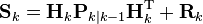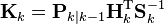KalmanFilter の動きを可視化する一次元版

KalmanFilter をきちんと理解したいのだがいまいち具体的な動作がわからない、、、ということで実装 & 可視化してみた。

KalmanFilter とは

誤差が乗っているであろう観測値の系列について、直前の観測と現在の観測を用いて真の状態を推定する手法。例えば

GPSで取得した位置情報から、正しい位置を推定する
取得可能な経済指標から真の景気の状態を推定する

カルマンフィルター - Wikipedia

理論

はてなの TeX 記法でうまく数式がかけないところがあるので英語版 wikipedia の数式を使う。KalmanFilter はある時点で観測を行うたびに入力値を使って次の状態を予測するとともに、現時点の予測値を補正する処理を繰り返す。

予測:

k-1 時点の値を利用して予測した k 時点での"真値の予測値" ${ \hat{x}_{k|k-1} }$

$http://upload.wikimedia.org/math/2/b/7/2b70a26158d36a9faa2b132ba7971419.png$
k-1 時点の値を利用して予測した k 時点での「真値と"真値の予測値"の誤差」の共分散 ${ P_{k|k-1} }$

$http://upload.wikimedia.org/math/8/8/8/8881cbcc105342ffce6653cc4671af9c.png$

更新:

k 時点での観測残差 (観測値と"真値の予測値から計算される観測値"の誤差) ${ \tilde{\boldsymbol{y}}_{k} }$

$http://upload.wikimedia.org/math/6/8/a/68ae03b8e5cccbcb1c1a7684721ad688.png$
k 時点での観測残差の共分散

$http://upload.wikimedia.org/math/b/9/a/b9a0989c597e32498b8e7e15e265bcd6.png$
カルマンゲイン (誤差 ${ P_{k|k-1} }$ を最小化する行列)

$http://upload.wikimedia.org/math/3/2/f/32f4d26fe53cfdde24f7cc50b303f5f6.png$
k 時点の値を利用して更新した k 時点での"真値の予測値" ${ \hat{x}_{k|k} }$

$http://upload.wikimedia.org/math/6/a/e/6ae5e6c89b215bf2a7630544773991c2.png$
k 時点の値を利用して更新した k 時点での「真値と"真値の予測値"の誤差」の共分散 ${ P_{k|k} }$

$http://upload.wikimedia.org/math/9/6/b/96b934387acd18af06506e491fd3a5e2.png$

単純化

とりあえず以下のように単純化する。

行列だとわけわからなくなるので、1次元で考える
真値は時間によって変化しない ( ${ F = 1 }$ , つまり ${ x_k = x_{k-1} }$ ) とする
システムへの入力はなし、つまり ${ u_k = 0 }$ とする
真値の誤差は時間変化しない ( ${ Q_k = Q_{k-1} }$ ) 、つまり定数とする
真値と観測値は同じ座標系 (この言葉がいいのかわかりませんが)、、、　つまり ${ H = 1 }$ とする

プログラム

元ネタは Python の Scipy cookbook。

Cookbook/KalmanFiltering -

set.seed(1)

# 観測系列のサンプルサイズ
n <- 120

# 真の値
actual <- 5

# 観測される値 (誤差は標準偏差2の正規分布とする)
observed <- rnorm(n, mean = actual, sd = 2)

# 結果保存用のvector
xhat <- rep(0, length.out = n)
P <- rep(0, length.out = n)
K <- rep(0, length.out = n)

# 誤差
Q = 1e-5
R = 0.1 ** 2

for (k in seq(2, n)) {
  # predict
  xhat.m <- xhat[k-1]
  P.m <- P[k-1] + Q

  # update
  S <- R + P.m
  K[k] <- P.m / S
  xhat[k] <- xhat.m + K[k] * (observed[k] - xhat.m)
  P[k] <- (1 - K[k]) * P.m
}

# 予測値の推移
xhat
#   [1] 0.000000000 0.005361925 0.011992113 0.036413891 0.058736991 0.075059292 0.109930176
#   [8] 0.153625564 0.200419955 0.236967065 0.311962013 0.369479486 0.408063382 0.410052292
# ...
#  [57] 3.584985506 3.565122418 3.641322662 3.673644005 3.856169061 3.887979061 3.962561981
#  [64] 3.995372573 3.980879247 4.022972720 3.943466256 4.064106742 4.101759405 4.260930294
# ...
# [106] 4.772249481 4.823831434 4.885835786 4.913247827 5.020455087 4.980316917 4.952240062
# [113] 5.042741558 5.000967888 4.988046417 4.963997727 4.945221799 4.929569956 4.962489912
# [120] 4.952628512

予測値 xhat は徐々に真値 5.0 に近づいていくことがわかる。

可視化

ggplot2 と animation パッケージで KalmanFilter の予測値が真値に近づいていく様子を可視化してみる。

library(animation)
library(ggplot2)

d <- data.frame(x = seq(1, n), actual = actual,
                observed = observed, 
                fitted = xhat, P = P, K = K)

saveGIF({
  for (i in seq(2, n, by = 2)) {
    tmp <- head(d, i)
    p <- ggplot(tmp, aes(x = x)) +
      geom_point(aes(y = observed)) +
      geom_line(aes(y = fitted), colour = 'blue') +
      annotate(geom = 'text', x = i, y = tmp$fitted[i] - 0.5,
               label = 'Fitted value', colour = 'blue', hjust = 1) +
      geom_line(aes(y = actual), colour = 'red') +
      annotate(geom = 'text', x = i, y = tmp$actual[i] + 0.5,
               label = 'True value', colour = 'red', hjust = 1) +
      ylim(-1, 8) +
      scale_x_continuous(breaks = seq(0, n, by = 20)) +
      xlab('') + ylab('')
    print(p)
  }
}, interval = 0.2, movie.name = "kalmanfilter01_01.gif",
ani.width = 600, ani.height = 400)

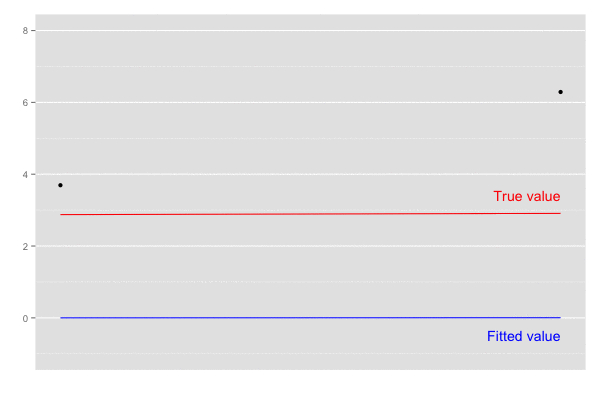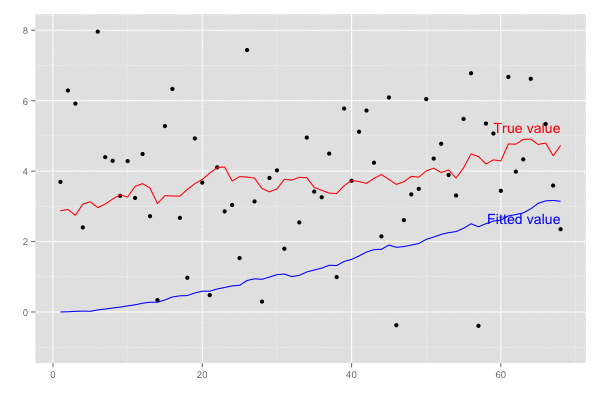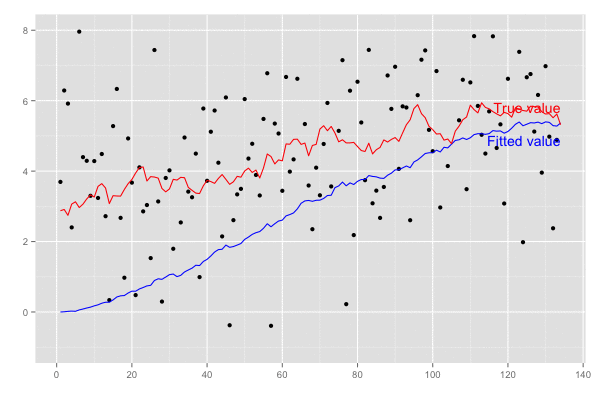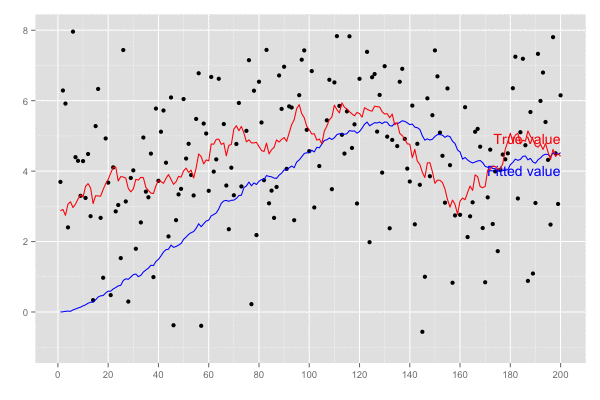
横軸を時間経過とし、観測値(黒点)が観測された際の予測値の推移(青線)を描画。

f:id:sinhrks:20141101174552g:plain

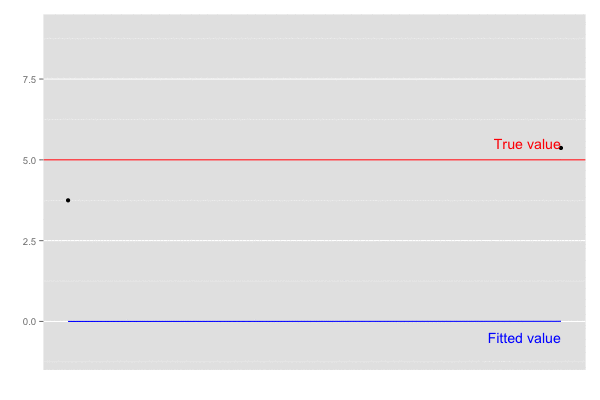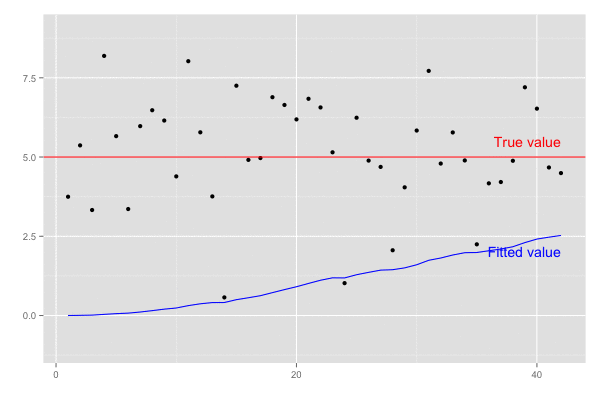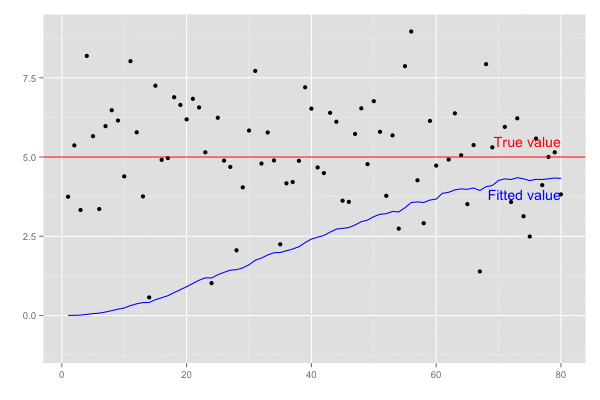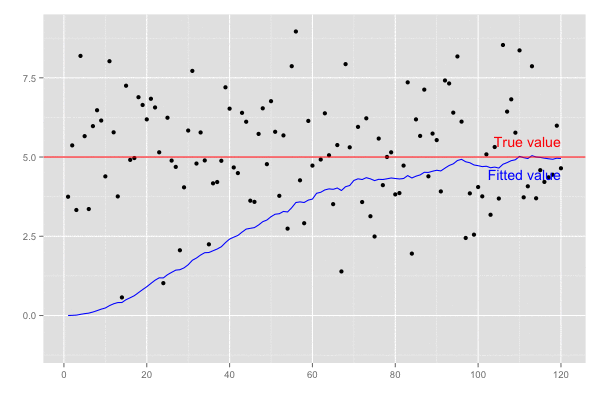
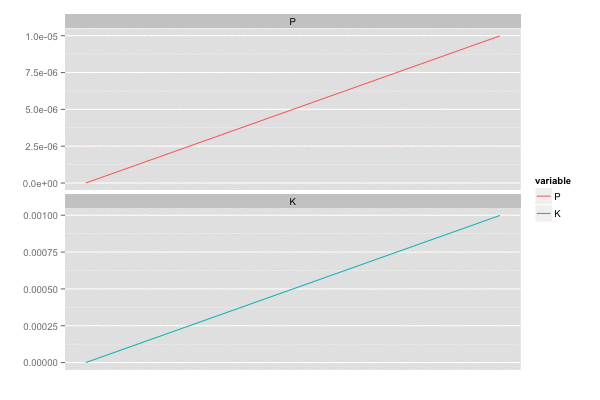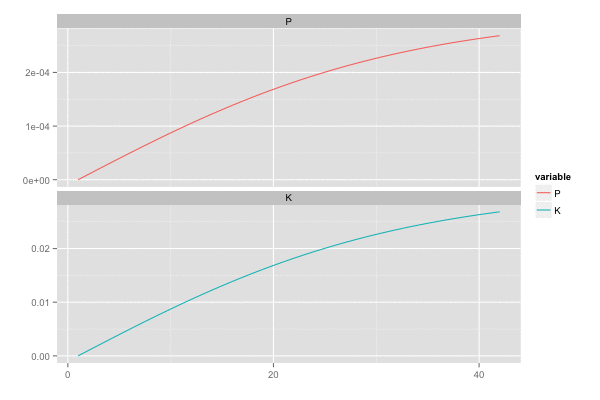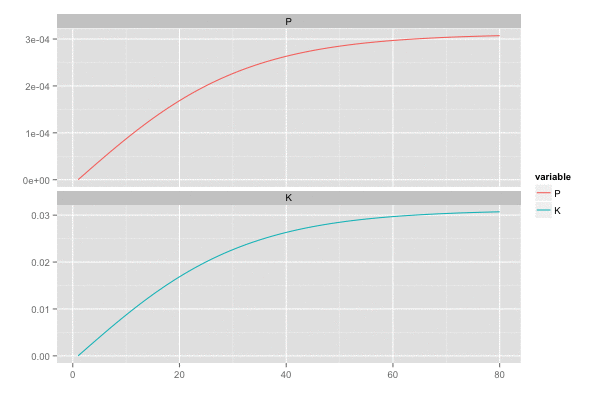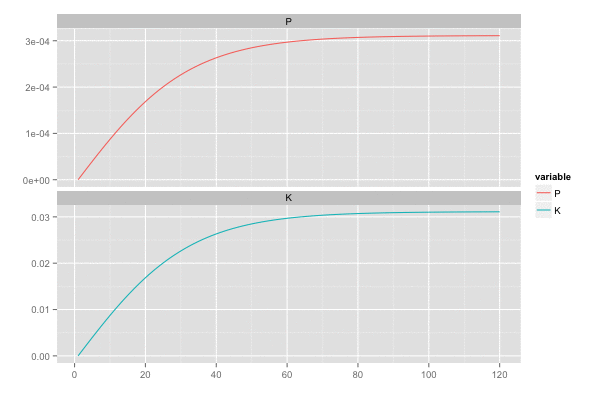
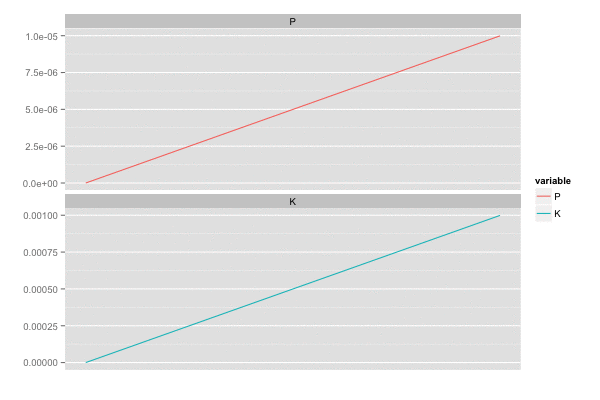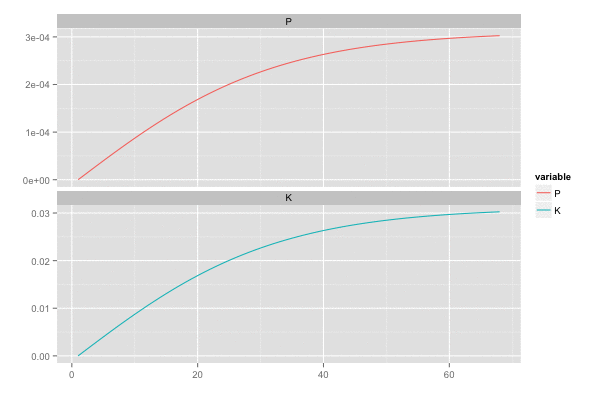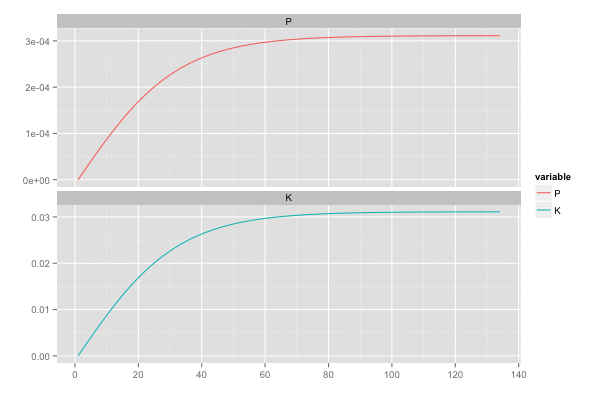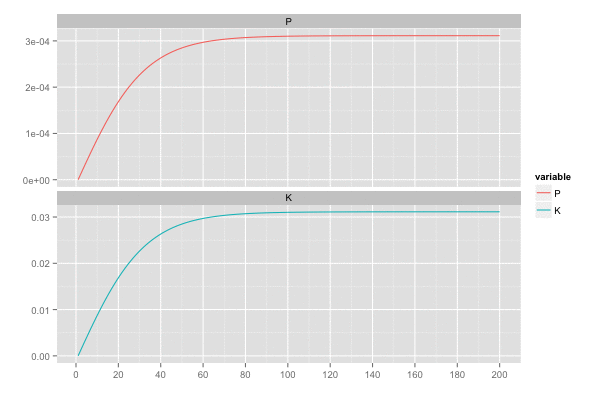
また、カルマンゲイン ${ K_k }$ は誤差の分散(一次元なので共分散はない) ${ P_k }$ を最小化しようとするので、 ${ H = 1 }$ のとき ${ K_k }$ , ${ P_k }$ は同じ動きをする。

library(tidyr)

saveGIF({
  for (i in seq(2, n, by = 2)) {
    tmp <- head(d, i)
    tmp <- gather(tmp, 'variable', 'value', c(P, K))
    p <- ggplot(tmp, aes(x = x, y = value, colour = variable)) +
      geom_line() + 
      facet_wrap(~ variable, ncol = 1, scale = 'free_y') +
      scale_x_continuous(breaks = seq(0, n, by = 20)) +
      xlab('') + ylab('')
    print(p)
  }
}, interval = 0.2, movie.name = "kalmanfilter02.gif",
ani.width = 600, ani.height = 400)

f:id:sinhrks:20141101180541g:plain

真値が時間によって変化する場合

真値を動かしてみる。

行列だとわけわからなくなるので、1次元で考える
真値の誤差は時間変化しない ( ${ Q_k = Q_{k-1} }$ ) 、つまり定数とする
真値と観測値は同じ座標系、つまり ${ H = 1 }$ とする

※真値は動かすが、KalmanFilterで予測はしない ( ${ F = 1 }$ , ${ u_k = 0 }$ は変わらず)

set.seed(1)

# 観測系列のサンプルサイズ
n <- 200

# 真の値が時間変化する
actual <- 3.0 + cumsum(rnorm(n, sd = 0.2))

# 観測される値 (誤差は標準偏差2の正規分布とする)
observed <- actual + rnorm(n, mean = 0, sd = 2)

# 以降同一