Python Dask で Out-Of-Core / 並列 LU 分解
はじめに
正方行列 を
となる下三角行列
と 上三角行列
に分解することを LU 分解という。LU 分解ができると連立方程式の解や逆行列が 前進/後退代入でかんたんに求められてうれしい。
Dask を使って LU 分解を Out-Of-Core / 並列でやりたい。
LU 分解の並列化にはいくつかやり方があるようで、東大講義 スパコンプログラミング(1)、スパコンプログラミング(I) の 第10回 LU分解法 にまとまっている。この講義、ガイダンス資料の単位取得状況を見るとかなり楽しそうな感じだ。
ここでは、Dask での実装がかんたんそうなブロック形式ガウス法 (資料 P33-) をやりたい。
ブロック形式ガウス法
ブロック形式ガウス法では入力となる行列をいくつかのブロックに区切り、ブロックごとに処理を行う。具体的には、左上の対角ブロックからはじめて、以下の順番で処理していく。
- 対角ブロックの計算
- 1と同じ行のブロックの計算
- 1と同じ列のブロックの計算
- 一つ右下の対角ブロックへ
処理の順序を図示すると以下のような形。行/列の処理 (2, 3) は順序関係ないため入れ替えてもよい = 並列に処理できる。
ブロック内の計算は 通常の (ブロック化しない) LU 分解や、基本的な行列演算の組み合わせで書ける。
上の PDF 資料では 3 ブロック目以降の式がよくわからないため、 行
列目のブロックを
として計算式を書いておく。
Python での実装を考慮して、逆行列ではなく scipy.linalg.solve (実際に使うのは solve_triangular ) を使って書く。
1. 対角ブロックの計算
※ は LU 分解を行う関数。
2. 1 と同じ行のブロックの計算
より、
※ は
を
について解く関数。
3. 1 と同じ列のブロックの計算
より、
Python での確認
具体的な処理を確かめるため、まず np.ndarray を手動でブロックに区切り、各ステップの計算を行う。
import numpy as np import scipy import scipy.linalg np.__version__ # '1.10.2' # 表示を丸め np.set_printoptions(precision=2) scipy.__version__ # '0.16.1'
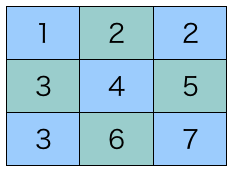
LU 分解する行列 は以下のようなものにした。ブロックの大きさを 3 x 3 にした時、計 9 個のブロックができる。
A = np.array([[ 9., 3., 7., 8., 8., 10., 3., 8., 6.], [ 2., 10., 10., 1., 8., 3., 7., 4., 8.], [ 7., 8., 1., 5., 7., 9., 5., 9., 2.], [ 1., 8., 6., 6., 10., 7., 7., 9., 3.], [ 8., 8., 10., 9., 5., 3., 7., 5., 4.], [ 1., 4., 3., 4., 3., 10., 3., 2., 1.], [ 4., 1., 6., 5., 4., 9., 10., 6., 9.], [ 6., 9., 2., 3., 8., 1., 9., 4., 2.], [ 8., 6., 2., 9., 8., 9., 3., 10., 8.]]) A

まずは ブロック化せずに LU 分解の結果を確かめる。LU 分解は scipy.linalg.lu で行うことができ、返り値は P, L, U の 3 つの ndarray となる。
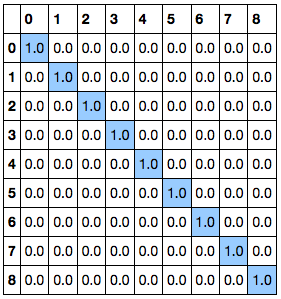
P は置換行列で、LU 分解時のピボット (行の入れ替え) 処理に対応する。今回は P が単位行列になっているため、ピボットなしで分解できていることがわかる。
P, L, U = scipy.linalg.lu(A) P
L, U
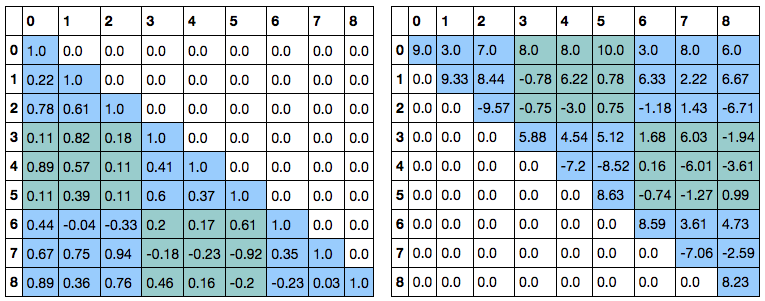
1. 対角ブロックの計算
まず、ndarray から i 行 j 列目のブロックを取り出す関数 block_slice を定義する。
def block_slice(m, i, j, size=3): return m[i*size:(i+1)*size, j*size:(j+1)*size] # 0 行 0 列目 A00 = block_slice(A, 0, 0) A00 # array([[ 9., 3., 7.], # [ 2., 10., 10.], # [ 7., 8., 1.]])
左上のブロック はそのまま LU 分解すればよい。LU 分解には
scipy.linalg.lu を使う。1 番目の返り値である P は単位行列となるため無視する。
_, L00, U00 = scipy.linalg.lu(A00) L00 # array([[ 1. , 0. , 0. ], # [ 0.22, 1. , 0. ], # [ 0.78, 0.61, 1. ]]) # 結果が一致するか確認。以降の出力は適宜省略 assert np.allclose(L00, block_slice(L, 0, 0)) assert np.allclose(U00, block_slice(U, 0, 0))
2. 1 と同じ行のブロックの計算
0 行目ならびに 0 列目では 上式の総和にあたる部分がないため、単に ,
を解けばよい。
は下三角行列であることから
scipy.linalg.solve_triangular で解ける。
# 0 行 1 列目 A01 = block_slice(A, 0, 1) U01 = scipy.linalg.solve_triangular(L00, A01, lower=True) U01 # array([[ 8. , 8. , 10. ], # [ -0.78, 6.22, 0.78], # [ -0.75, -3. , 0.75]]) # 0 行 2 列目 A02 = block_slice(A, 0, 2) U02 = scipy.linalg.solve_triangular(L00, A02, lower=True) assert np.allclose(U01, block_slice(U, 0, 1)) assert np.allclose(U02, block_slice(U, 0, 2))
3. 1 と同じ列のブロックの計算
こちらも上式そのまま。
# 1 行 0 列目 A10 = block_slice(A, 1, 0) L10 = scipy.linalg.solve_triangular(U00.T, A10.T, lower=True).T L10 # array([[ 0.11, 0.82, 0.18], # [ 0.89, 0.57, 0.11], # [ 0.11, 0.39, 0.11]]) # 2 行 0 列目 A20 = block_slice(A, 2, 0) L20 = scipy.linalg.solve_triangular(U00.T, A20.T, lower=True).T assert np.allclose(L10, block_slice(L, 1, 0)) assert np.allclose(L20, block_slice(L, 2, 0))
4. 一つ右下の対角ブロックへ
# 1 行 1 列目 A11 = block_slice(A, 1, 1) _, L11, U11 = scipy.linalg.lu(A11 - L10.dot(U01)) L11 # array([[ 1. , 0. , 0. ], # [ 0.41, 1. , 0. ], # [ 0.6 , 0.37, 1. ]]) assert np.allclose(L11, block_slice(L, 1, 1)) assert np.allclose(U11, block_slice(U, 1, 1))
以降、上式と同じ処理を続ける。
# 1 行 2 列目 A12 = block_slice(A, 1, 2) U12 = scipy.linalg.solve_triangular(L11, A12 - L10.dot(U02), lower=True) assert np.allclose(U12, block_slice(U, 1, 2)) # 2 行 1 列目 A21 = block_slice(A, 2, 1) L21 = scipy.linalg.solve_triangular(U11.T, (A21 - L20.dot(U01)).T, lower=True).T assert np.allclose(L21, block_slice(L, 2, 1)) # 2 行 2 列目 A22 = block_slice(A, 2, 2) _, L22, U22 = scipy.linalg.lu(A22 - L20.dot(U02) - L21.dot(U12)) L22 # array([[ 1. , 0. , 0. ], # [ 0.35, 1. , 0. ], # [-0.23, 0.03, 1. ]]) assert np.allclose(L22, block_slice(L, 2, 2)) assert np.allclose(U22, block_slice(U, 2, 2))
ここまでで、ブロック形式ガウス法の具体的な処理が確かめられた。
置換行列 P の処理
P は行の入れ替えに対応するので、"2. 対角ブロックと同じ行のブロックの計算" を行う前後で P を考慮した変換をすればよい。置換行列の逆行列は転置と一致する ( ) ため、
inv や solve は不要。
Dask での実装
Dask では計算処理を以下のような DAG で定義する。定義したグラフは Dask のスケジューラによって自動的に Out-Of-Core / 並列処理される。ブロック形式ガウス法では行/列の処理 (2, 3) や、各ブロック内での計算中に出てくる行列積は 順序関係ないため並列で実行できる。
上の処理を Dask のグラフとして書き直すと以下のようになる。置換行列 P の処理も追加している。
# 利用するには1/23以降のmaster (公式には 0.7.6 の次のバージョン) が必要 dA = da.from_array(A, (3, 3)) dP, dL, dU = da.linalg.lu(dA) assert np.allclose(dL.compute(), L) assert np.allclose(dU.compute(), U) # 結果は上と同一のため略 dL.visualize()
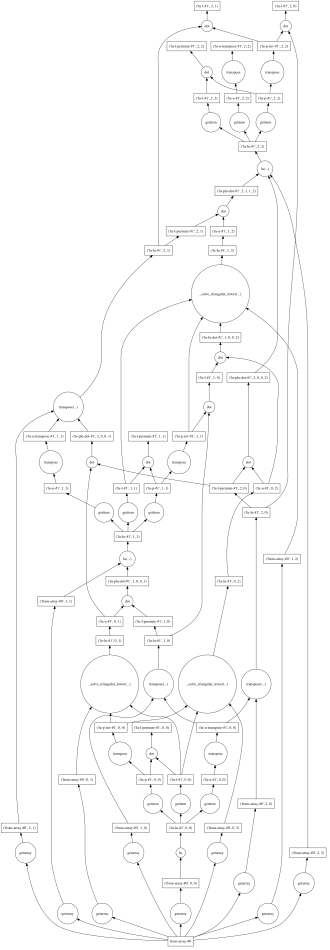
まとめ
ブロック形式ガウス法の処理方法を確認し、Dask での実装を行った。LU 分解の結果を利用すると、連立方程式の解や逆行列も Out-Of-Core / 並列で求めることができる。
- ENH: add da.linalg.solve by sinhrks · Pull Request #938 · blaze/dask · GitHub
- ENH: add da.linalg.inv by sinhrks · Pull Request #939 · blaze/dask · GitHub

- 作者: 片桐孝洋
- 出版社/メーカー: 東京大学出版会
- 発売日: 2013/03/13
- メディア: 単行本
- この商品を含むブログを見る