Python pandas 欠損値/外れ値/離散化の処理

データの前処理にはいくつかの工程がある。書籍「データ分析プロセス」には 欠損など 前処理に必要なデータ特性の考慮とその対処方法が詳しく記載されている。

が、書籍のサンプルは R なので、Python でどうやればよいかよく分からない。同じことを pandas でやりたい。

データ分析プロセス (シリーズ Useful R 2)

とはいえ、pandas 自身は統計的 / 機械学習的な前処理手法は持っていない。また Python には R と比べると統計的な前処理手法のパッケージは少なく、自分で実装しないと使えない方法も多い。ここではそういった方法は省略し、pandas でできる前処理 / 可視化を中心に書く。

また、方法自体の説明は記載しないので、詳細を知りたい方は 「データ分析プロセス」を読んでください。

データの要約

import numpy as np
import pandas as pd
pd.__version__
# u'0.17.1'

import matplotlib.pyplot as plt
import seaborn as sns

データの特徴をつかむため、要約統計量や相関係数が見たい。ここでは 「データ分析プロセス」と同じく Iris データ (scikit-learn に含まれているもの / 書籍とは少し値が違う) を例として使う。

import sklearn.datasets as datasets
iris_data = datasets.load_iris()

iris = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
iris['species'] = iris_data.target
iris.head()

変数の要約 (要約統計量)

pandas での要約統計量の表示は DataFrame.describe。5 列目 "species" も数値型だが、カテゴリ変数のため除外する。

iris.iloc[:, :4].describe()

"species" についてはラベルごとの頻度が見たいので Series.value_counts で集計する。

iris['species'].value_counts()
# 2    50
# 1    50
# 0    50
# Name: species, dtype: int64

2 変数の関係 (相関係数と散布図行列)

また、相関係数の表示は DataFrame.corr。

iris.iloc[:, :4].corr()

散布図行列を描くには seaborn.pairplot。"species" に応じて色分けして描画する。

sns.pairplot(iris, hue='species');

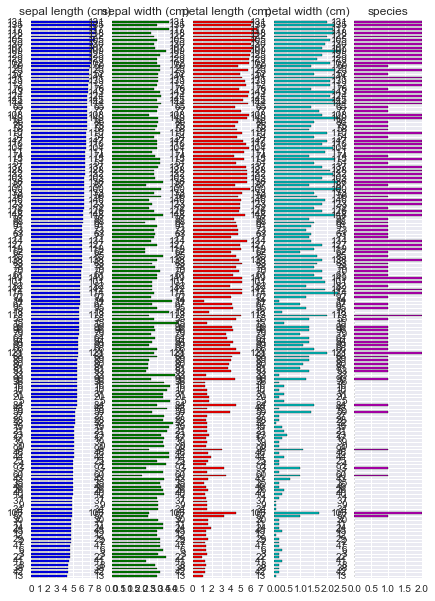
また、R には {tabplot} という data.frame 可視化のためのパッケージがある。これに近い出力は pandas でもかんたんに得られる。

(iris.sort_values('sepal length (cm)').
 plot.barh(subplots=True, layout=(1, 5), sharex=False, legend=False));

欠損値

「データ分析プロセス」で使われているサンプルデータ employee_IQ_JP.csv を使う。ファイルは出版社のサポートページ からダウンロードできる。

データは知能指数 "IQ" と業務成果 "JobPerformance" 2 つの変数の関係を示している。3 列目以降は "JobPerformance" が以下いずれかのパターンで欠損した場合の例を示している。

欠損発生のパターン	概要
MCAR	ランダムに欠損している ( 欠損は "IQ" や "JobPerformance" の値に関係しない )
MAR	他の変数の値と関係して欠損している ( "IQ" が低いと "JobPerformance" の欠損が多い )
MNAR	欠損が発生しているデータ自身と関係して欠損している ( "JobPerformance" の真の値が低いと "JobPerformance" の欠損が多い )

df = pd.read_csv('employee_IQ_JP.csv')
df.head()

欠損パターンの可視化

欠損がそれぞれのパターンで発生した場合に、真の値 "JobPerformance" のうち欠損値となった箇所を 赤三角 "▲" で描く。

fig, axes = plt.subplots(1, 3)
fig.tight_layout(w_pad=2.0)
for col, ax in zip(['MCAR', 'MAR', 'MNAR'], axes):
    indexer = df[col].isnull()
    df[indexer].plot.scatter(x='IQ', y='JobPerformance', marker='^',
                             color='red', label='missing', ax=ax)
    df[~indexer].plot.scatter(x='IQ', y='JobPerformance', ax=ax)
    ax.set_title(col)

次に、上よりもカラム数が多いサンプルデータを使って欠損のパターンを可視化する例を示す。R の {mice} パッケージから、nhanes データセットを CSV に出力し、pandas で読み込む。

• nhanes {mice} | inside-R | A Community Site for R

nhances = pd.read_csv('nhanes.csv', index_col=0)
nhances.head()

上の通り複数の変数で欠損が発生している。欠損がどのように発生しているかを調べるには以下のように集計すればよい。

missing = nhances.copy()
# 欠損している場合に True とする
missing = missing.apply(pd.isnull, axis=0)
missing['count'] = 1
missing.groupby(['age', 'bmi', 'hyp', 'chl']).sum()

この結果から以下のことがわかる。

• 欠損がない (全て False ) レコードは 13件 )
• "chl" のみ欠損している ( "chl"のみ True ) レコードは 3 件
• 以下略

また、変数別に欠損しているレコード数を調べるには sum を取ればよい。

missing[['age', 'bmi', 'hyp', 'chl']].sum()
# age     0
# bmi     9
# hyp     8
# chl    10
# dtype: int64

また、ある 2 つの変数 "bmi", "hyp" を選んで、欠損がどのように発生しているかを調べたい。DataFrame.pivot_table で集計する。

missing.pivot_table(index='hyp', columns='bmi', values='count', aggfunc='sum')

この結果から、

• 2 変数とも欠損なし: 16 件
• "bmi" のみ欠損: 1 件
• 以下略

上で調べた欠損値の発生状況をプロットすると以下のようになる。

• 左側: 各変数が欠損しているレコード数
• 右側: 欠損している変数の組み合わせごとのレコード数

fig, axes = plt.subplots(1, 3)
missing[['age', 'bmi', 'hyp', 'chl']].sum().plot.bar(ax=axes[0])
missing.groupby(['age', 'bmi', 'hyp', 'chl']).sum().plot.barh(ax=axes[2])
axes[1].set_visible(False);

また、変数 "age" について、自身以外の変数 "bmi", "hyp", "chl" がそれぞれが欠損した / しなかった場合の分布を箱ヒゲ図で描く。 "age" の値が 他の変数の欠損とどのような関係にあるかがわかる。

missing['age'] = nhances['age']
fig, axes = plt.subplots(1, 4)
fig.tight_layout(w_pad=3.0)
sns.boxplot(data=missing, y='age', ax=axes[0])
sns.boxplot(data=missing, y='age', x='bmi', ax=axes[1])
sns.boxplot(data=missing, y='age', x='hyp', ax=axes[2])
sns.boxplot(data=missing, y='age', x='chl', ax=axes[3]);

欠損に対する処理

欠損値に対する対応にはいくつかの方法がある。うち、pandas, scikit-learn でできる方法を記載する。

方法	概要
リストワイズ法	欠損レコードを除去
ペアワイズ法	相関係数など 2 変数を用いて計算を行う際に、対象の変数が 欠損している場合に計算対象から除外
平均代入法	欠損を持つ変数の平均値を補完
回帰代入法	欠損を持つ変数の値を 回帰式をもとに補完

完全情報最尤推定、多重代入は Python にはなさそうなので、使うなら R のパッケージを呼び出すしかないと思う。

リストワイズ法

リストワイズ法では欠損を除去すれば良いため DataFrame.dropna でできる。

nhances.shape
# (25, 4)

nhances.dropna(subset=['bmi']).shape
# (16, 4)

nhances.dropna(subset=['bmi', 'chl'], how='any').shape
# (13, 4)

ペアワイズ法

少し手間がかかるが、対象となる 2 変数について欠損しているレコードを除去 -> 計算を繰り返せばできる。

平均代入法

平均代入のように代表値で埋める場合は DataFrame.fillna。

nhances['bmi']
# 1      NaN
# 2     22.7
# 3      NaN
# 4      NaN
#        ...
# 24    24.9
# 25    27.4
# Name: bmi, dtype: float64

nhances['bmi'].fillna(nhances['bmi'].mean())
# 1     26.5625
# 2     22.7000
# 3     26.5625
# 4     26.5625
#         ...
# 24    24.9000
# 25    27.4000
# Name: bmi, dtype: float64

回帰代入法

回帰代入では欠損が発生している変数と 欠損の発生に影響している変数とで回帰式を作り、作られた回帰式を使って欠損を補完する。欠損は MAR で発生していないとダメ。サンプルデータとしては 再び employee_IQ_JP.csv を使う。

回帰には scikit-learn を使う。当たり前だが補間された値は回帰直線 (灰色破線) 上に乗る。

import sklearn.linear_model as lm
reg = lm.LinearRegression()
indexer = df['MAR'].isnull()
reg.fit(df.loc[~indexer, ['IQ']], df.loc[~indexer, 'MAR'])
predicted = reg.predict(df.loc[indexer, ['IQ']])
df.loc[indexer, 'MAR'] = predicted

# プロット
ax = df[indexer].plot.scatter(x='IQ', y='MAR', marker='^', color='red', label='missing');
ax = df[~indexer].plot.scatter(x='IQ', y='MAR', ax=ax);
x = np.linspace(*ax.get_xlim())
ax.plot(x, reg.coef_[0] * x + reg.intercept_, color='gray', linestyle='dashed')

外れ値

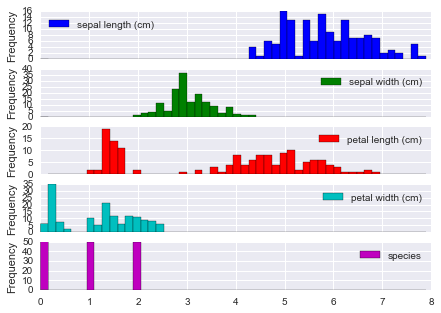
外れ値をみるにはまずデータの分布 / 箱ヒゲ図を描くのがかんたん。

iris.plot(kind='hist', bins=50, subplots=True);

四分位範囲での検出

seaborn.boxplot では 外れ値はダイヤ "♦︎" で描画される。外れ値とみなす閾値は whis オプションを利用して指定できる。既定は 1.5 で、四分位範囲 (IQR) = 第3四分位 - 第1四分位 の 1.5 倍を超えるレコードが外れ値となる。

ここでは "species" のラベルごとに、各変数の箱ヒゲ図を描く。

fig, axes = plt.subplots(3, 1)
for i, (n, g) in enumerate(iris.groupby('species')):
    sns.boxplot(data=g.iloc[:, :4], ax=axes[i])
    axes[i].set_ylabel(n)

「データ分析プロセス」に記載されているその他の方法のうち、LOF (Local Outlier Factor) には Python のパッケージがあるが、メンテされているか謎だ。

また、scikit-learn の 1 クラス SVM や ガウス過程 を使う方法もある。これらは 機械学習プロフェッショナルシリーズ「状態変化と異常検知」に記載がある。

方法	Python パッケージ / リンク
LOF	damjankuznar/pylof - Python - GitHub
1 クラス SVM	Outlier detection with several methods. — scikit-learn 0.17 documentation
ガウス過程	Robust Regression and Outlier Detection via Gaussian Processes | Bugra Akyildiz

異常検知と変化検知 (機械学習プロフェッショナルシリーズ)

離散化

以下 2 つの方法については pandas でできる。

方法	概要
等間隔区間 (EWD)	対象のカラムの値を等間隔の区分で分割する
等頻度区間 (EFD)	分割した区分に同程度の数のレコードが含まれるように分割する

等間隔区間による離散化

等間隔区間による離散化は pd.cut。どのように分割されたかは categories として表示される。

pd.cut(iris['sepal length (cm)'], 5)
# 0       (5.02, 5.74]
# 1      (4.296, 5.02]
#            ...      
# 148     (5.74, 6.46]
# 149     (5.74, 6.46]
# Name: sepal length (cm), dtype: category
# Categories (5, object): [(4.296, 5.02] < (5.02, 5.74] < (5.74, 6.46] < (6.46, 7.18] < (7.18, 7.9]]

区分ごとのレコード数を数えるには Series.value_counts。結果を Series.sort_index して区分の順番に並べている。

pd.cut(iris['sepal length (cm)'], 5).value_counts().sort_index()
# (4.296, 5.02]    32
# (5.02, 5.74]     41
# (5.74, 6.46]     42
# (6.46, 7.18]     24
# (7.18, 7.9]      11
# dtype: int64

等頻度区間による離散化

等頻度区間による離散化は pd.qcut。

pd.qcut(iris['sepal length (cm)'], 5)
# 0         (5, 5.6]
# 1         [4.3, 5]
#           ...     
# 148    (6.1, 6.52]
# 149     (5.6, 6.1]
# Name: sepal length (cm), dtype: category
# Categories (5, object): [[4.3, 5] < (5, 5.6] < (5.6, 6.1] < (6.1, 6.52] < (6.52, 7.9]]

pd.qcut(iris['sepal length (cm)'], 5).value_counts().sort_index()
# [4.3, 5]       32
# (5, 5.6]       33
# (5.6, 6.1]     30
# (6.1, 6.52]    25
# (6.52, 7.9]    30
# dtype: int64

「データ分析プロセス」に記載されているその他の方法のうち、最小記述長原理 (MDLP) での離散化は scikit-learn に PR が上がっている。

方法	Python パッケージ / リンク
最小記述長原理 (MDLP)	Discretization using Fayyad's MDLP stop criterion by hlin117 · Pull Request #4801 · scikit-learn/scikit-learn · GitHub

まとめ

書籍「データ分析プロセス」の流れに沿って、欠損値/外れ値/離散化の処理を、pandas で行う方法を記載した。

上で記載した方法 = Python でできる方法は書籍の内容のうち比較的 簡単な方法だけだ。より網羅的に知りたい方は書籍を読んでいただくのがいい。R ユーザに限らずおすすめ。

データ分析プロセス (シリーズ Useful R 2)