KalmanFilter の動きを可視化する二次元版

こちらのつづき。一次元での動きはわかってきたので、今回は二次元でやってみる + KalmanFilter の予測 F を入れてみる。

<a href="http://sinhrks.hatenablog.com/entry/2014/11/01/231333">KalmanFilter の動きを可視化する一次元版 - StatsFragments</a>

二次元への拡張

まず以下の条件で考える。

二変数は ${ x, y}$ とし、それぞれ独立に動く
観測誤差はそれぞれの成分で独立
真値の予測, システムの入力はなし ( ${ F = I_2 }$ , ${ u_k = 0 }$ )
真値の誤差は時間変化しない ( ${ Q_k = Q_{k-1} }$ )
真値と観測値は同じ座標系 ( ${ H = I_2 }$ )

※アニメーション部分のコードはちょっと汚いので省略 / gist に添付。

set.seed(1)

# 観測系列のサンプルサイズ
n <- 100

# 真の値
x <- c(rep(0, n / 4), seq(0, 10, length.out = n / 4),
       rep(10, n / 4), seq(10, 0, length.out = n / 4))
y <- c(seq(0, 10, length.out = n / 4), rep(10, n / 4),
       seq(10, 0, length.out = n / 4), rep(0, n / 4))
actual <- cbind(x, y)

# 観測系列の次元
dim <- ncol(actual)

# 観測される値 (誤差は標準偏差0.1の独立正規分布とする)
observed <- actual + matrix(rnorm(n * dim, sd = 0.1), ncol = dim)

# 結果保存用のmatrix
xhat <- matrix(0, nrow = n, ncol = dim)

# 結果保存用の array
# P[, , k] K[, , k] に 時刻 k 時点の計算結果を保存
P <- array(c(0.0, 0.1, 0, 0.1), dim = c(dim, dim, n))
K <- array(0, dim = c(dim, dim, n))

# 誤差
Q <- diag(0.01, nrow = dim, ncol = dim)
R <- diag(0.01, nrow = dim, ncol = dim)

# 単位行列
I <- diag(1, ncol = dim, nrow = dim)

for (k in seq(2, n)) {
  # predict
  xhat.m <- xhat[k-1, ]
  P.m <- P[, , k-1] + Q
  
  # update
  S <- R + P.m
  K[, , k] <- P.m %*% solve(S)
  xhat[k, ] <- xhat.m + K[, , k] %*% (observed[k, ] - xhat.m)
  P[, , k] <- (I - K[, , k]) * P.m
}

x, y の動きをプロットすると以下のようになる (赤が真の値、黒が観測値、青がKalmanFilterの予測値)。

上段のグラフは二変数 x, y について平面上にプロットしたもの。
下段の2つのグラフは、 x, y それぞれが時間 (time) に対してどのように動くかをプロットしたもの。

f:id:sinhrks:20141104235735g:plain

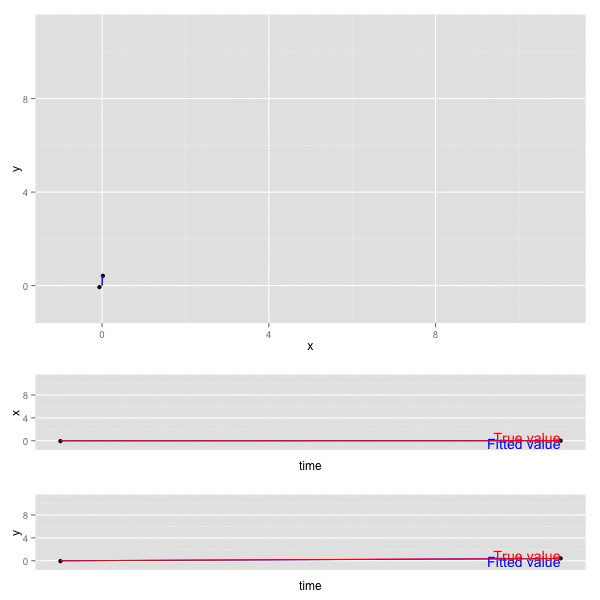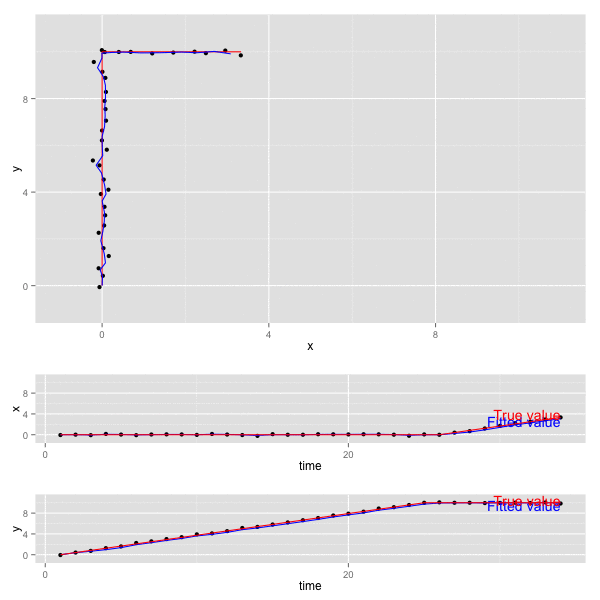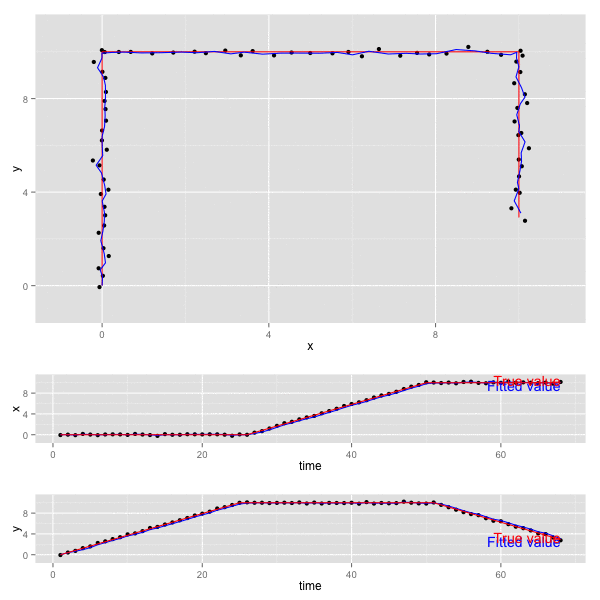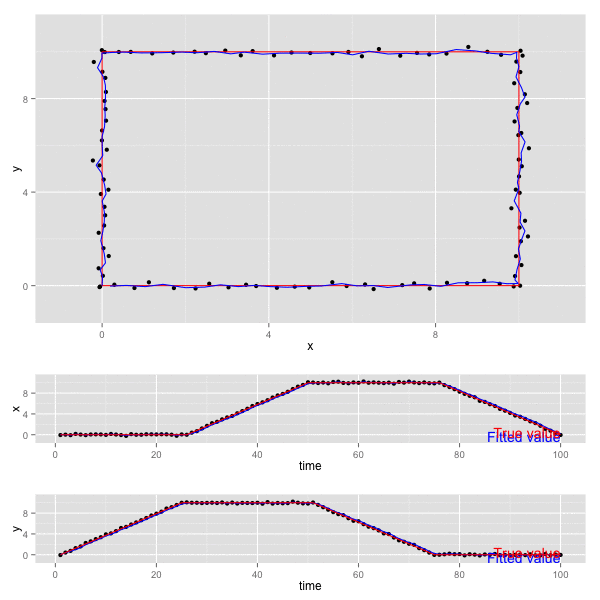
誤差の共分散 P , カルマンゲイン K は最終的に以下の値となっていた。観測誤差が独立なので、共分散成分はでてこない。

P[, , 100]
#            [,1]       [,2]
# [1,] 0.00618034 0.00000000
# [2,] 0.00000000 0.00618034

K[, , 100]
#          [,1]     [,2]
# [1,] 0.618034 0.000000
# [2,] 0.000000 0.618034

多次元になった場合も、それぞれの系列が独立で相互に干渉しなければ、各系列は 1次元の場合と同じ動きをする (各系列をわけて考えることができる)。

KalmanFilter の予測 F を入れる

これまでの例では ${ F = I_2 }$ と考えていたため、KalmanFilter の予測部分 (以下の式) で予測値が更新されることはなかった (正確にいうと Q のみ計算されていた)。今度は F による予測ステップでの計算も含めて、各系列がどのように動くのか見てみる。

予測ステップ:

$http://upload.wikimedia.org/math/2/b/7/2b70a26158d36a9faa2b132ba7971419.png$

$http://upload.wikimedia.org/math/8/8/8/8881cbcc105342ffce6653cc4671af9c.png$

日本語版 wikipedia の "設定例" に記載されているトロッコの例をもとに実装する。

加速度 0.5 で等加速度運動するトロッコの位置 x, 速さ v を考える
観測誤差はそれぞれの成分で独立
真値の予測 ${ F = \begin{bmatrix} 1　1 \\ 0　1 \end{bmatrix} }$ つまり、k+1時点のx = ${ x_k + v_k }$ , K+1時点のv = ${ v_k }$ と予測する
システムの入力はなし ( ${ u_k = 0 }$ )
真値の誤差は時間変化しない ( ${ Q_k = Q_{k-1} }$ )
真値と観測値は同じ座標系 ( ${ H = I_2 }$ )

set.seed(1)

# 観測系列のサンプルサイズ
n <- 30

# 加速度
a <-rep(0.3, n)

v <- cumsum(0.5 * a)
x <- cumsum(v)

# 真の値
actual <- data.frame(x = x, v = v)

# 観測系列の次元
dim <- ncol(actual)

# 観測される値 (誤差は独立正規分布とする)
observed <- cbind(x + 0.5 * rnorm(n, sd = 0.05),
                  v + rnorm(n, sd = 0.05))

# 予測結果保存用のmatrix
xhat.m <- matrix(0, nrow = n, ncol = dim)
# 補正結果保存用のmatrix
xhat <- matrix(0, nrow = n, ncol = dim)

# F
FM <- matrix(c(1, 0, 1, 1), ncol = 2)

# 結果保存用の array
# P[, , k] K[, , k] に 時刻 k 時点の計算結果を保存
P <- array(c(0.0, 0.1, 0, 0.1), dim = c(dim, dim, n))
K <- array(0, dim = c(dim, dim, n))

# 誤差
Q <- diag(0.01, nrow = dim, ncol = dim)
R <- diag(0.01, nrow = dim, ncol = dim)

# 単位行列
I <- diag(1, ncol = dim, nrow = dim)

for (k in seq(2, n)) {
  # predict
  xhat.m[k, ] <- FM %*% xhat[k-1, ]
  P.m <- FM %*% P[, , k-1] %*% t(FM) + Q
  
  # update
  S <- R + P.m
  K[, , k] <- P.m %*% solve(S)
  xhat[k, ] <- xhat.m[k, ] + K[, , k] %*% (observed[k, ] - xhat.m[k, ])
  P[, , k] <- (I - K[, , k]) * P.m
}

x, vをそれぞれ x軸, y軸方向にとり、以下のステップを順にプロットしてみた。

k - 1 の観測値をもとにして時刻 k の予測値を計算 (青破線) -> 予測ステップに該当
時刻 k の値を観測 (黒点)
時刻 k の値により、観測値を補正 (青実線) -> 更新ステップに該当

1で計算された予測値が、観測2をうけて補正され、3での更新後は真の値(赤線)に近づいた値となっていることがわかる。

f:id:sinhrks:20141104235639g:plain

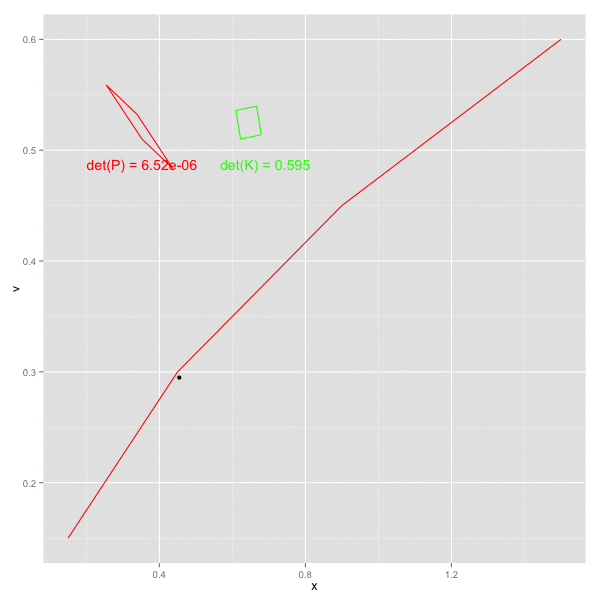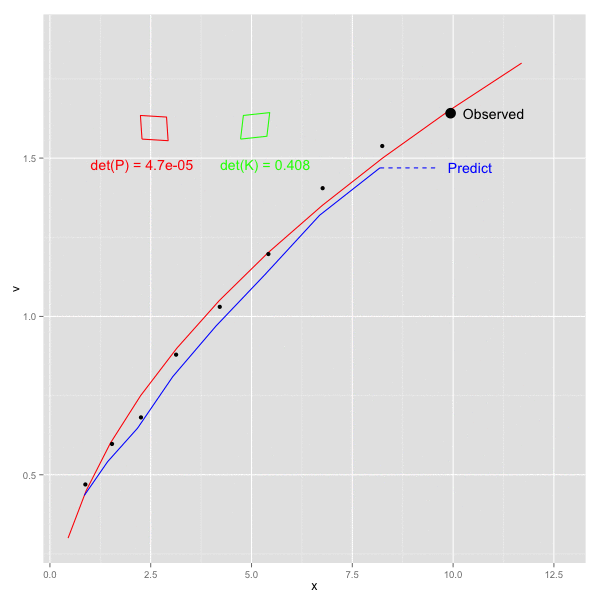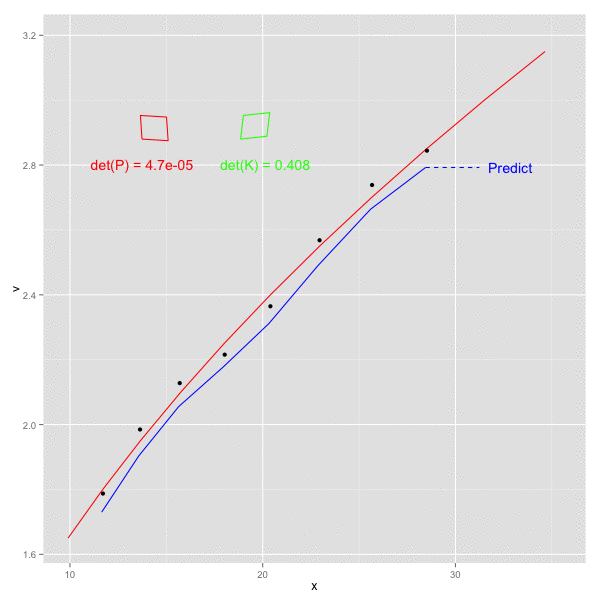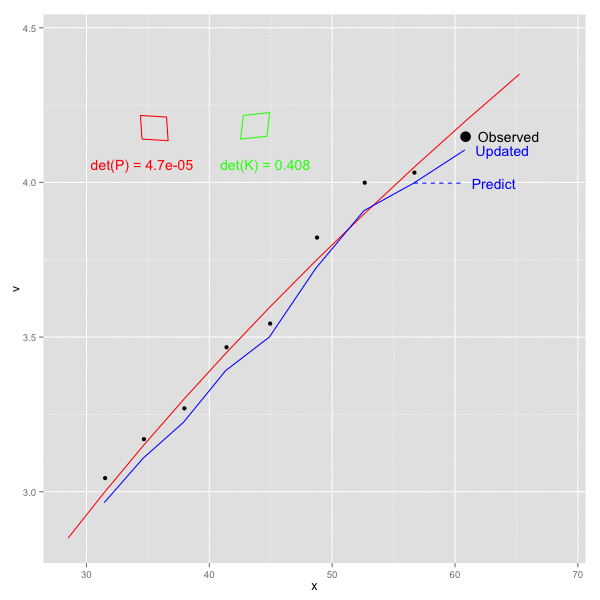
また、画面左側の赤四角、緑の四角はそれぞれ、誤差の共分散 P とカルマンゲイン K の各行列を四角形への回転として図示したもの。四角形は若干傾いており、P, K ともに共分散成分が含まれることを示す ( 実際にデータに乗せている誤差は独立だが、予測ステップで P が F によって更新される際に共分散があらわれてくる)。

今回で KalmanFilter の予測、更新のステップはだいぶわかってきた (気がする)。が、まだ誤差についての理解が怪しいな、、。