PyStan で「StanとRでベイズ統計モデリング」11.3節
著者の松浦さんから「StanとRでベイズ統計モデリング」をいただきました。ありがとうございます!
書籍では Stan の R バインディングである RStan を利用していますが、Stan には Python 用の PyStan もあります。松浦さんが書籍 5.1節の PyStan での実行例を書かれています。
補足 PyStan については過去にも書いた内容があります。
同じように、「StanとRでベイズ統計モデリング」の内容を Python で実施してみました。
11.3 ゼロ過剰ポアソン分布
以降、書籍 "11.3節 ゼロ過剰ポアソン分布" の流れに沿って Python のスクリプトを記載します。ロジックや処理自体の説明は書籍をご参照ください。データと Stan のスクリプトは GitHub上の StanとRでベイズ統計モデリング サポートページ から取得できます。
ゼロ過剰ポアソン分布とは: ポアソン分布と比べ、ゼロの割合が多い分布。ベルヌーイ分布 x ポアソン分布の混合分布としてモデル化できる。
import os import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns pd.__version__ # '0.19.0' sns.__version__ # '0.7.1'
ダウンロードしたデータを読み込みます。
df = pd.read_csv(os.path.join('input', 'data-ZIP.txt')) df
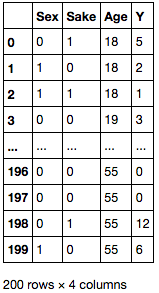
Y 列の分布を確認すると、0 が多く含まれていることがわかります。
ax = df['Y'].plot.hist() df['Y'].plot.kde(grid=False, ax=ax.twinx());
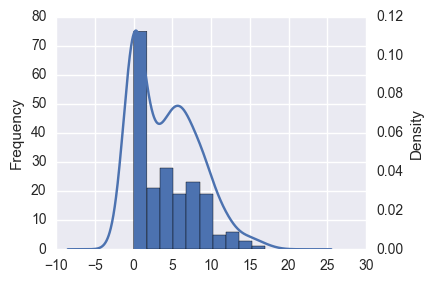
このような場合、重回帰をしても決定係数が低く、予測結果の分布も明らかに異なっています。
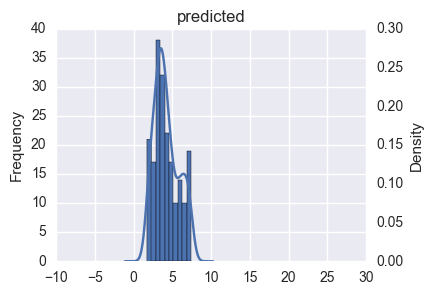
import pandas_ml as pdml mdf = pdml.ModelFrame(df, target='Y') lm = mdf.lm.LinearRegression() mdf.fit(lm) # LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) # 決定係数 mdf.score(lm) # 0.14312960776740502 # 切片, 回帰係数 lm.intercept_, lm.coef_ # (2.2039889528112147, array([-1.32283473, 2.65683543, 0.04619692])) ax = predicted.plot.hist() predicted.plot.kde(title='predicted', grid=False, ax=ax.twinx(), xlim=(-10, 30));
データの分布の確認
上で見たとおり、データはカテゴリ値 ( 離散値、Sex, Sake) と 連続値 ( Age, Y ) が混ざったデータとなっています。
R には {GGally} というパッケージがあり、値の種類に応じて散布図行列中のプロットを描きわけてくれます。
Python で似たようなことをするには、seaborn の PairGrid クラスを使うのが良いでしょう。PairGrid クラスは与えられたデータの散布図行列に必要なサブプロットを生成し、それぞれの成分に対して適当なプロット関数をまとめて適用することができます。
seaborn 標準では値の種類に応じたプロットの描きわけができないので、自作のプロット関数を用意します。設定変更を容易にするため、Dispatcher クラスとして作成しました。上三角部分は(ほぼ)松浦さんのブログのそのままです。
class Dispatcher(object): def __init__(self, fontsize=20, alpha=0.6, cmap='RdBu', threshold=10): self.fontsize = fontsize self.alpha = alpha self.cmap = plt.get_cmap(cmap) # 離散値 / 連続値とみなす閾値 self.threshold = threshold def comb(self, x_series, y_series, label=None, color=None): """ 下三角部分のプロット """ x_nunique = x_series.nunique() y_nunique = y_series.nunique() if x_nunique < self.threshold and y_nunique < self.threshold: # 離散値 x 離散値のプロット return self._dd_plot(x_series, y_series, label=label, color=color) elif x_nunique < self.threshold or y_nunique < self.threshold: # 離散値 x 連続値のプロット return self._dc_plot(x_series, y_series, label=label, color=color) else: # 連続値 x 連続値のプロット return plt.scatter(x_series, y_series, label=label, color=color) def _dd_plot(self, x_series, y_series, label=None, color=None): """ 離散値 x 離散値のプロット """ # x, y 各組み合わせの個数を集計 total = y_series.groupby([x_series, y_series]).count() # x, y軸をプロットする位置を取得 xloc = total.index.labels[0] yloc = total.index.labels[1] values = total.values ax = plt.gca() for xp, yp, vp in zip(xloc, yloc, values): ax.annotate(vp, (xp, yp), fontsize=self.fontsize, ha='center', va='center') # 組み合わせの個数を散布図としてプロット size = values / (values.max() * 1.1) * 100 * 20 ax.scatter(xloc, yloc, s=size, label=label, color=color) ax.set_ylim(yloc[0] - 0.5, yloc[-1] + 0.5) def _dc_plot(self, x_series, y_series, label=None, color=None): """ 離散値 x 連続値のプロット """ if y_series.nunique() < x_series.nunique(): # y軸が離散値の場合は、x, yを入替 # 水平方向に箱ひげ図をプロット x_series, y_series = y_series, x_series vert = False else: vert = True xlab, xun = pd.factorize(x_series) # 箱ひげ図用のデータの準備 data = [] for i, g in y_series.groupby(xlab): data.append(g) ax = plt.gca() ax.boxplot(data, positions=np.arange(len(data)), vert=vert) # 散布図をプロット xloc = xlab + np.random.normal(scale=0.05, size=len(xlab)) if not vert: y_series, xloc = xloc, y_series ax.scatter(xloc, y_series, label=label, color=color, alpha=self.alpha) def diag(self, series, label=None, color=None): """ 対角部分のプロット """ ax = series.plot.hist() ax = series.plot.kde(grid=False, ax=ax.twinx()) ax.yaxis.set_visible(False) def ellipse(self, x_series, y_series, label=None, color=None): """ 上三角部分のプロット """ from matplotlib.patches import Ellipse # 相関係数を楕円としてプロット r = x_series.corr(y_series) c = self.cmap(0.5 * (r + 1)) ax = plt.gca() ax.axis('off') ax.add_artist(Ellipse(xy=[.5, .5], width=np.sqrt(1 + r), height=np.sqrt(1 - r), angle=45, facecolor=c, edgecolor='none', transform=ax.transAxes)) ax.text(.5, .5, '{:.0f}'.format(r * 100), fontsize=self.fontsize, ha='center', va='center', transform=ax.transAxes)
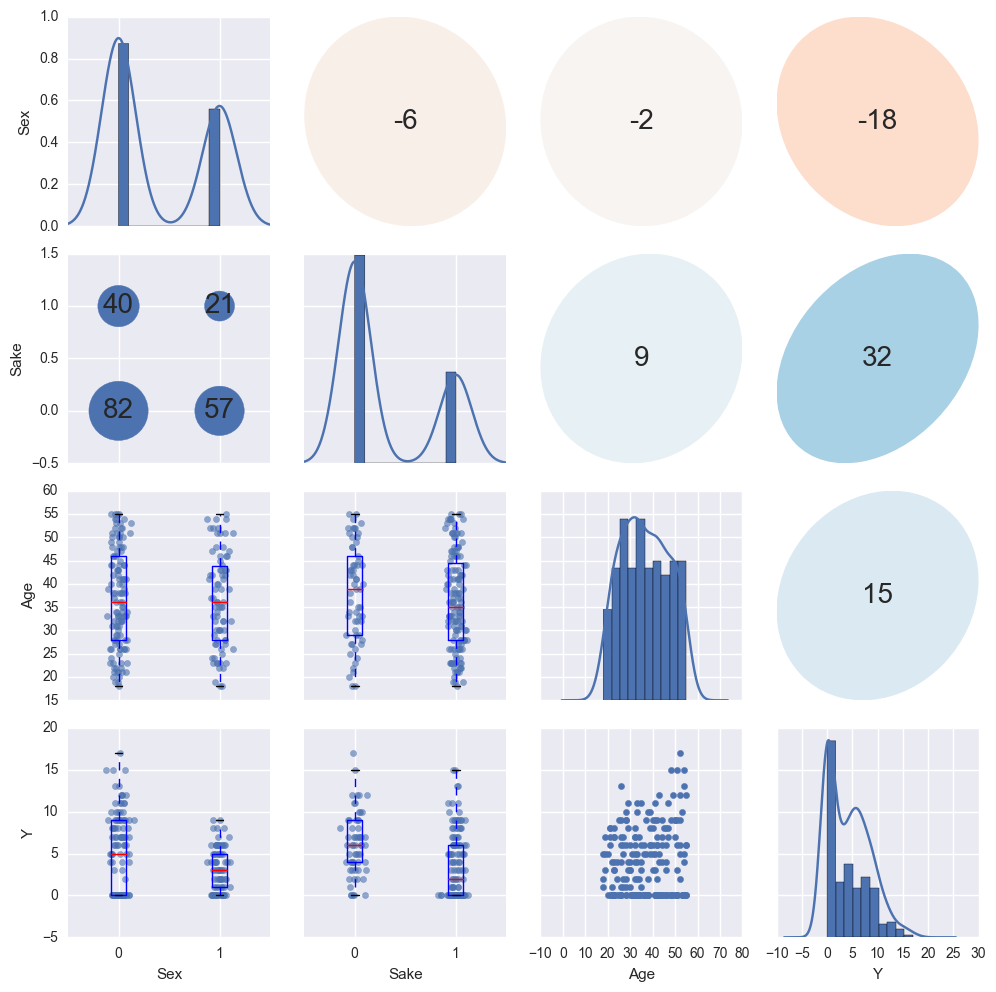
作成したクラスを使ってプロットします。対角成分にはヒストグラムを描画する = y 軸が他と異なるため、PairGrid の作成時に
diag_sharey=False を指定します。
g = sns.PairGrid(df, diag_sharey=False) d = Dispatcher() # 対角成分 g.map_diag(d.diag) # 下三角成分 g.map_lower(d.comb); # 上三角成分 g.map_upper(d.ellipse);
Stanの実行
ここから、PyStan を使ってサンプリングを行います。
import pystan pystan.__version__ # '2.12.0.0'
Age 列のスケールを変更し、切片に対応する列を挿入します。
df['Age'] = df['Age'] / 10 X = df[['Sex', 'Sake', 'Age']] X.insert(0, 'Intercept', 1) X
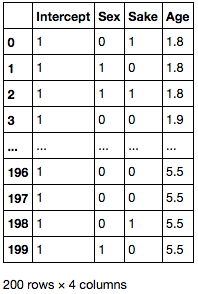
PyStan でサンプリングを実施します。書籍とは添字や表示順序が異なります。
stanmodel = pystan.StanModel(file='model/model11-7.stan') # INFO:pystan:COMPILING THE C++ CODE FOR MODEL anon_model_f3132948938ed3766129342e203c72d6 NOW. data = {'N': X.shape[0], 'D': X.shape[1], 'X': X.values, 'Y': df['Y'].values} fit = stanmodel.sampling(data=data, pars=['b', 'q', 'lambda'], seed=123) fit # Inference for Stan model: anon_model_f3132948938ed3766129342e203c72d6. # 4 chains, each with iter=2000; warmup=1000; thin=1; # post-warmup draws per chain=1000, total post-warmup draws=4000. # # mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat # b[0,0] 0.95 0.01 0.66 -0.37 0.51 0.95 1.39 2.27 2434 1.0 # b[1,0] 1.45 2.9e-3 0.13 1.2 1.36 1.44 1.54 1.7 2080 1.0 # b[0,1] 1.61 7.7e-3 0.42 0.82 1.32 1.6 1.89 2.46 2978 1.0 # b[1,1] -0.75 1.4e-3 0.08 -0.9 -0.8 -0.75 -0.69 -0.6 3159 1.0 # b[0,2] 3.36 0.02 0.86 2.01 2.78 3.24 3.81 5.3 1647 1.0 # b[1,2] -0.16 1.4e-3 0.07 -0.31 -0.21 -0.16 -0.11 -0.02 2648 1.0 # b[0,3] -0.37 3.6e-3 0.17 -0.72 -0.49 -0.37 -0.25 -0.03 2355 1.0 # b[1,3] 0.2 7.4e-4 0.03 0.13 0.18 0.2 0.22 0.26 2020 1.0 # ... 略 ...
q と lambda の順位相関係数の信用区間を求めます。サンプルごとに相関係数を求め、分位点を取ればよいです。
samples = fit.extract() from scipy import stats r = [stats.spearmanr(x, y)[0] for x, y in zip(samples['q'], samples['lambda'])] np.percentile(r, q=[2.5, 25, 50, 75, 97.5]) # array([-0.80461466, -0.6961319 , -0.64964589, -0.6052952 , -0.47924492])
まとめ
- 「StanとRでベイズ統計モデリング」11章3節を
PyStanでやってみました RStanとPyStanで大きな機能差はないので、前処理 / 後処理 (プロット) に慣れている言語を使えばいいと思います- 書名は "StanとRで..." となっていますが、複雑な
Rコードは出てきません (本エントリの "Stanで実行" 部分がわかれば読める程度です)。そのため、統計モデリングに興味があるPythonユーザにもおすすめです

StanとRでベイズ統計モデリング (Wonderful R)
- 作者: 松浦健太郎,石田基広
- 出版社/メーカー: 共立出版
- 発売日: 2016/10/25
- メディア: 単行本
- この商品を含むブログ (4件) を見る
Python でパイプ演算子を使いたい <2>
ネタ記事です。/ This is a joke post which makes no practical sense.
過去にこんなエントリを書いた。
R では パイプ演算子 %>% を使って連続した処理を記述できる。式に含まれる
x, y, z は非標準評価 (NSE) によって data.frame の列として解決される。
# R (magrittr + dplyr) df %>% mutate(x = y + z) %>% group_by(x) %>% summarize_each(funs(sum))
Python (pandas) ではほぼ同じ処理をメソッドチェインを使って書ける。チェインとパイプ演算子でどちらが読みやすいかは好みの問題だと思うものの、式の中に 何度も df が出てくるのはちょっとすっきりしない。
# Python (pandas) df.assign(x=df['y'] + df['z']).groupby('x').sum()
上の式をこんな風に書けるとうれしい。
df >> assign(x=y+z) >> groupby(x) >> sum()
前のエントリでは マジックメソッドと関数定義で近いことをやったが、以下のような課題がある。
- パイプ演算子で処理したいメソッドを、それぞれ関数として別に定義しなければならない
- R の非標準評価のようなことはできない (ある変数を別の環境で評価することができない)
前者は手間をかければなんとかなるが、後者については NameError が発生してしまうためどうしようもない。
df.assign(x=y+z)
# NameError: name 'y' is not defined
上のような表現を式に含めるには、 lambda を使って無名関数にすればよい。lambda を使うと、下のように定義されていない関数 / 変数を式に含めることができる。
lambda: df >> assign(x=y+z) # <function <lambda> at 0x102310620>
当然、この無名関数をそのまま評価すると NameError が発生する。定義した無名関数の中身を調べて、妥当な処理に置き換えてやればよい。
Python 標準では ast モジュールを使って 抽象構文木 (AST) の探索や置換ができる。が、今回はそこまで複雑なことをやるわけではないので、バイトコードを直接書き換えられるとうれしい。
バイトコードの置換について簡単な方法がないか調べたところ CodeTransformer というパッケージを見つけた。今回はこれを使いたい。
CodeTransformerとは
バイトコードに対するパターンマッチ⇨置換が簡単にできる。詳しい使い方はドキュメントを。
まずは関数がバイトコードとしてどのように表現されているのか確かめたい。これは標準の dis モジュールを使うのが簡単。
import dis dis.dis(lambda x: x + 2) # 1 0 LOAD_FAST 0 (x) # 3 LOAD_CONST 1 (2) # 6 BINARY_ADD # 7 RETURN_VALUE
CodeTransformer を使うと適当なパターンにマッチするバイトコードを置換することができる。ドキュメントの例にある通り、バイトコード中の加算 (BINARY_ADD) を乗算 (BINARY_MULTIPLY) に置き換える CodeTransformer は以下のようになる。
import codetransformer codetransformer.__version__ # '0.6.0' from codetransformer import CodeTransformer, pattern from codetransformer.instructions import BINARY_ADD, BINARY_MULTIPLY class Multiply(CodeTransformer): @pattern(BINARY_ADD) def _add2mul(self, add_instr): yield BINARY_MULTIPLY().steal(add_instr)
pattern デコレータで指定したバイトコードにマッチした時、対応したメソッドが呼び出される。呼び出されるメソッドから置換後のバイトコードを返せばよい。
作成した CodeTransformer を使って関数を置換する。
mul = Multiply()(lambda x: x + 2) mul(5) # 10
Multiply によって置き換えられた後のバイトコードを確認すると、BINARY_ADD が BINARY_MULTIPLY に置換されていることが確かめられる。
dis.dis(mul) # 1 0 LOAD_FAST 0 (x) # 3 LOAD_CONST 0 (2) # 6 BINARY_MULTIPLY # 7 RETURN_VALUE
パイプ演算子を使いたい
ここから、pandas と組み合わせて使ってみる。まずはデータを準備する。
import pandas as pd df = pd.DataFrame({'A': [1, 2, 3, 4, 5, 6], 'B': list('ABABAB'), 'C': [1, 2, 3, 1, 2, 3]}) df # A B C # 0 1 A 1 # 1 2 B 2 # 2 3 A 3 # 3 4 B 1 # 4 5 A 2 # 5 6 B 3
パイプ演算子を処理するには、lambda: df >> head() のバイトコードを lambda: df.head() のバイトコードに置換すればよい。置換前、置換後のバイトコードをそれぞれ確認すると、
# 置換前 dis.dis(lambda: df >> head()) # 1 0 LOAD_GLOBAL 0 (df) # 3 LOAD_GLOBAL 1 (head) # 6 CALL_FUNCTION 0 (0 positional, 0 keyword pair) # 9 BINARY_RSHIFT # 10 RETURN_VALUE # 置換後 dis.dis(lambda: df.head()) # 1 0 LOAD_GLOBAL 0 (df) # 3 LOAD_ATTR 1 (head) # 6 CALL_FUNCTION 0 (0 positional, 0 keyword pair) # 9 RETURN_VALUE
比べてみると、以下のような変換を行えばよさそうだ。
- 置換前のパターン:
LOAD_GLOBAL → CALL_FUNCTION → BINARY_RSHIFT - 置換後のパターン:
LOAD_ATTR → CALL_FUNCTION
連続したパターンとマッチさせるには、pattern デコレータと対応するメソッドに複数の引数を指定すればよい。
from codetransformer.instructions import BINARY_RSHIFT, LOAD_GLOBAL, LOAD_ATTR, CALL_FUNCTION class Pipify(CodeTransformer): @pattern(LOAD_GLOBAL, CALL_FUNCTION, BINARY_RSHIFT) def _pipe(self, load, call, rshift): # LOAD_GLOBAL を LOAD_ATTR に置換 yield LOAD_ATTR(load.arg) yield call # BINARY_SHIFT は無視
これにパイプ演算を含む無名関数を渡すと、期待通り動いているように見える。
Pipify()(lambda: df >> head())() # A B C # 0 1 A 1 # 1 2 B 2 # 2 3 A 3 # 3 4 B 1 # 4 5 A 2 dis.dis(Pipify()(lambda: df >> head())) # 1 0 LOAD_GLOBAL 0 (df) # 3 LOAD_ATTR 1 (head) # 6 CALL_FUNCTION 0 (0 positional, 0 keyword pair) # 9 RETURN_VALUE
もっとも、上のクラスは非常に単純な条件でしか動かない。たとえば、パイプで接続される関数(メソッド)に引数がある場合、patternの定義とマッチしなくなるため置換が行われない。
# NG Pipify()(lambda: df >> head(2))() # NameError: name 'head' is not defined dis.dis(lambda: df >> head(2)) # 1 0 LOAD_GLOBAL 0 (df) # 3 LOAD_GLOBAL 1 (head) # 6 LOAD_CONST 1 (2) # 9 CALL_FUNCTION 1 (1 positional, 0 keyword pair) # 12 BINARY_RSHIFT # 13 RETURN_VALUE
もう少しマシな CodeTransformer の定義を考える。パイプ演算子の記法から、 LOAD_GLOBAL から次の BINARY_RSHIFT までを 1 単位とした pattern 定義でマッチすればよいような気がする。
CodeTransformer の定義は以下のようになる。(~BINARY_RSHIFT)[plus] は BINARY_SHIFT 以外の任意のコードの繰り返しとマッチする。
from codetransformer import plus class Pipify(CodeTransformer): @pattern(LOAD_GLOBAL, (~BINARY_RSHIFT)[plus], BINARY_RSHIFT) def _pipe(self, load, *args): # メソッド呼び出しの処理 if hasattr(self, 'first_load'): yield LOAD_ATTR(load.arg) else: # 最初の LOAD_GLOBAL は置き換えない self.first_load = load yield load # メソッドへの引数の処理 for arg in args[:-1]: if isinstance(arg, LOAD_GLOBAL): # 関数の一番最初の LOAD_GLOBAL から解決 # この定義では、パイプ演算中に更新されたデータやグローバル変数には # アクセスできない yield self.first_load yield LOAD_ATTR(arg.arg) else: yield arg # 末尾は BINARY_RSHIFT なので無視
コメントで "メソッドへの引数の処理" とある部分は、 (記載のとおり限定的だが) R の非標準評価に近い処理になる。
この定義を使うと、上で失敗したメソッド呼び出しも処理できる。
Pipify()(lambda: df >> head(2))() # A B C # 0 1 A 1 # 1 2 B 2 dis.dis(Pipify()(lambda: df >> head(2))) # 1 0 LOAD_GLOBAL 0 (df) # 3 LOAD_GLOBAL 0 (df) # 6 LOAD_ATTR 1 (head) # 9 LOAD_CONST 0 (2) # 12 CALL_FUNCTION 1 (1 positional, 0 keyword pair) # 15 RETURN_VALUE
いちいち Pipify()(lambda: df >> ...)() と書くのは面倒なので、パイプ演算を開始する関数 p を定義する。この関数を使うとパイプ演算は p(lambda: df >> ...) のように書ける。
def p(expr): return Pipify()(expr)()
以下、いくつかのパターンを試す。それぞれ、冒頭にコメントとして記載した処理と同じ結果になる。
# df.head() p(lambda: df >> head()) # A B C # 0 1 A 1 # 1 2 B 2 # 2 3 A 3 # 3 4 B 1 # 4 5 A 2 # df.head(2) p(lambda: df >> head(2)) # A B C # 0 1 A 1 # 1 2 B 2
パイプ演算中の B は NameError とはならず df.B として解決される (非標準評価もどき)。
# df.groupby(df.B).sum() p(lambda: df >> groupby(B) >> sum()) # A C # B # A 9 6 # B 12 6
もう少し複雑な処理もできる。.assign で df.A + df.C の結果からなる X 列を新規で作成し、B 列の値ごとに集約して合計を取る。
# df.assign(X=df.A+df.C).groupby(df.B).sum() p(lambda: df >> assign(X=A+C) >> groupby(B) >> sum()) # A C X # B # A 9 6 15 # B 12 6 18
改行を含む場合は括弧で囲む。
p(lambda: (df >> assign(X=A+C) >> groupby(B) >> sum())) # 略
まとめ
CodeTransformerでバイトコードを置換することで、パイプ演算のような処理が書ける。また、非標準評価に近いこともできる。- R を使ったほうがいい。
PyConJP 2016: pandasでの時系列処理についてお話させていただきました
21日、22日と PyCon JP に参加させていただきました。ご参加いただいた皆様、スタッフの皆様ありがとうございました。資料はこちらになります。
pandas による時系列データ処理
pandas を使った時系列データの前処理と、statsmodels での時系列モデリングの触りをご紹介しました。
時系列モデルの考え方については全く説明していないので、以下書籍などをご参照ください。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)
- 作者: 沖本竜義
- 出版社/メーカー: 朝倉書店
- 発売日: 2010/02/01
- メディア: 単行本
- 購入: 4人 クリック: 101回
- この商品を含むブログ (6件) を見る
元ネタ
以下のエントリをベースに新しい内容を追加しています。
時系列モデルを含む Python パッケージ
トーク中では ARIMA などの時系列モデルを含むパッケージとして statsmodels についてご説明、PyFlux をご紹介しました。一方 変化点検知や異常検知では、広く使われている Python パッケージはありません。
というわけで、作りました。現状、以下の2手法が実装されています。適当に手法追加しつつ、そのうちblogも書きます。
- 累積和法による変化点検知: R の
{changepoint}の実装と同一 - 成分分解 + Generalized ESD test による異常検知: R の
{AnomalyDetection}の実装に近いもの (同じではない)
補足 statsmodels v0.9ではマルコフ転換モデルが実装予定。また、skyline という異常検知アプリはあります。
Python pandas 欠損値/外れ値/離散化の処理
データの前処理にはいくつかの工程がある。書籍「データ分析プロセス」には 欠損など 前処理に必要なデータ特性の考慮とその対処方法が詳しく記載されている。
が、書籍のサンプルは R なので、Python でどうやればよいかよく分からない。同じことを pandas でやりたい。

- 作者: 福島真太朗,金明哲
- 出版社/メーカー: 共立出版
- 発売日: 2015/06/25
- メディア: 単行本
- この商品を含むブログ (2件) を見る
とはいえ、pandas 自身は統計的 / 機械学習的な前処理手法は持っていない。また Python には R と比べると統計的な前処理手法のパッケージは少なく、自分で実装しないと使えない方法も多い。ここではそういった方法は省略し、pandas でできる前処理 / 可視化を中心に書く。
また、方法自体の説明は記載しないので、詳細を知りたい方は 「データ分析プロセス」を読んでください。
データの要約
import numpy as np import pandas as pd pd.__version__ # u'0.17.1' import matplotlib.pyplot as plt import seaborn as sns
データの特徴をつかむため、要約統計量や相関係数が見たい。ここでは 「データ分析プロセス」と同じく Iris データ (scikit-learn に含まれているもの / 書籍とは少し値が違う) を例として使う。
import sklearn.datasets as datasets iris_data = datasets.load_iris() iris = pd.DataFrame(iris_data.data, columns=iris_data.feature_names) iris['species'] = iris_data.target iris.head()

変数の要約 (要約統計量)
pandas での要約統計量の表示は DataFrame.describe。5 列目
"species" も数値型だが、カテゴリ変数のため除外する。
iris.iloc[:, :4].describe()

"species" についてはラベルごとの頻度が見たいので Series.value_counts で集計する。
iris['species'].value_counts() # 2 50 # 1 50 # 0 50 # Name: species, dtype: int64
2 変数の関係 (相関係数と散布図行列)
また、相関係数の表示は DataFrame.corr。
iris.iloc[:, :4].corr()

散布図行列を描くには seaborn.pairplot。"species" に応じて色分けして描画する。
sns.pairplot(iris, hue='species');

また、R には {tabplot} という data.frame 可視化のためのパッケージがある。これに近い出力は pandas でもかんたんに得られる。
(iris.sort_values('sepal length (cm)'). plot.barh(subplots=True, layout=(1, 5), sharex=False, legend=False));
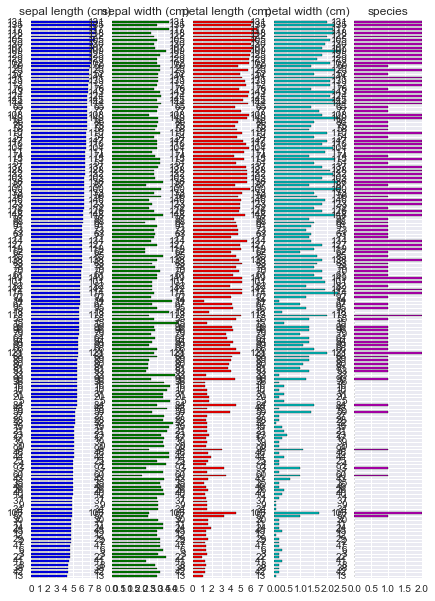
欠損値
「データ分析プロセス」で使われているサンプルデータ employee_IQ_JP.csv を使う。ファイルは出版社のサポートページ からダウンロードできる。
データは知能指数 "IQ" と業務成果 "JobPerformance" 2 つの変数の関係を示している。3 列目以降は "JobPerformance" が以下いずれかのパターンで欠損した場合の例を示している。
| 欠損発生のパターン | 概要 |
|---|---|
| MCAR | ランダムに欠損している ( 欠損は "IQ" や "JobPerformance" の値に関係しない ) |
| MAR | 他の変数の値と関係して欠損している ( "IQ" が低いと "JobPerformance" の欠損が多い ) |
| MNAR | 欠損が発生しているデータ自身と関係して欠損している ( "JobPerformance" の真の値が低いと "JobPerformance" の欠損が多い ) |
df = pd.read_csv('employee_IQ_JP.csv')
df.head()

欠損パターンの可視化
欠損がそれぞれのパターンで発生した場合に、真の値 "JobPerformance" のうち欠損値となった箇所を 赤三角 "▲" で描く。
fig, axes = plt.subplots(1, 3) fig.tight_layout(w_pad=2.0) for col, ax in zip(['MCAR', 'MAR', 'MNAR'], axes): indexer = df[col].isnull() df[indexer].plot.scatter(x='IQ', y='JobPerformance', marker='^', color='red', label='missing', ax=ax) df[~indexer].plot.scatter(x='IQ', y='JobPerformance', ax=ax) ax.set_title(col)

次に、上よりもカラム数が多いサンプルデータを使って欠損のパターンを可視化する例を示す。R の {mice} パッケージから、nhanes データセットを CSV に出力し、pandas で読み込む。
nhances = pd.read_csv('nhanes.csv', index_col=0) nhances.head()

上の通り複数の変数で欠損が発生している。欠損がどのように発生しているかを調べるには以下のように集計すればよい。
missing = nhances.copy() # 欠損している場合に True とする missing = missing.apply(pd.isnull, axis=0) missing['count'] = 1 missing.groupby(['age', 'bmi', 'hyp', 'chl']).sum()

この結果から以下のことがわかる。
- 欠損がない (全て
False) レコードは 13件 ) - "chl" のみ欠損している ( "chl"のみ
True) レコードは 3 件 - 以下略
また、変数別に欠損しているレコード数を調べるには sum を取ればよい。
missing[['age', 'bmi', 'hyp', 'chl']].sum() # age 0 # bmi 9 # hyp 8 # chl 10 # dtype: int64
また、ある 2 つの変数 "bmi", "hyp" を選んで、欠損がどのように発生しているかを調べたい。DataFrame.pivot_table で集計する。
missing.pivot_table(index='hyp', columns='bmi', values='count', aggfunc='sum')

この結果から、
- 2 変数とも欠損なし: 16 件
- "bmi" のみ欠損: 1 件
- 以下略
上で調べた欠損値の発生状況をプロットすると以下のようになる。
- 左側: 各変数が欠損しているレコード数
- 右側: 欠損している変数の組み合わせごとのレコード数
fig, axes = plt.subplots(1, 3) missing[['age', 'bmi', 'hyp', 'chl']].sum().plot.bar(ax=axes[0]) missing.groupby(['age', 'bmi', 'hyp', 'chl']).sum().plot.barh(ax=axes[2]) axes[1].set_visible(False);

また、変数 "age" について、自身以外の変数 "bmi", "hyp", "chl" がそれぞれが欠損した / しなかった場合の分布を箱ヒゲ図で描く。 "age" の値が 他の変数の欠損とどのような関係にあるかがわかる。
missing['age'] = nhances['age'] fig, axes = plt.subplots(1, 4) fig.tight_layout(w_pad=3.0) sns.boxplot(data=missing, y='age', ax=axes[0]) sns.boxplot(data=missing, y='age', x='bmi', ax=axes[1]) sns.boxplot(data=missing, y='age', x='hyp', ax=axes[2]) sns.boxplot(data=missing, y='age', x='chl', ax=axes[3]);

欠損に対する処理
欠損値に対する対応にはいくつかの方法がある。うち、pandas, scikit-learn でできる方法を記載する。
| 方法 | 概要 |
|---|---|
| リストワイズ法 | 欠損レコードを除去 |
| ペアワイズ法 | 相関係数など 2 変数を用いて計算を行う際に、対象の変数が 欠損している場合に計算対象から除外 |
| 平均代入法 | 欠損を持つ変数の平均値を補完 |
| 回帰代入法 | 欠損を持つ変数の値を 回帰式をもとに補完 |
完全情報最尤推定、多重代入は Python にはなさそうなので、使うなら R のパッケージを呼び出すしかないと思う。
リストワイズ法
リストワイズ法では欠損を除去すれば良いため DataFrame.dropna でできる。
nhances.shape # (25, 4) nhances.dropna(subset=['bmi']).shape # (16, 4) nhances.dropna(subset=['bmi', 'chl'], how='any').shape # (13, 4)
ペアワイズ法
少し手間がかかるが、対象となる 2 変数について欠損しているレコードを除去 -> 計算を繰り返せばできる。
平均代入法
平均代入のように代表値で埋める場合は DataFrame.fillna。
nhances['bmi'] # 1 NaN # 2 22.7 # 3 NaN # 4 NaN # ... # 24 24.9 # 25 27.4 # Name: bmi, dtype: float64 nhances['bmi'].fillna(nhances['bmi'].mean()) # 1 26.5625 # 2 22.7000 # 3 26.5625 # 4 26.5625 # ... # 24 24.9000 # 25 27.4000 # Name: bmi, dtype: float64
回帰代入法
回帰代入では欠損が発生している変数と 欠損の発生に影響している変数とで回帰式を作り、作られた回帰式を使って欠損を補完する。欠損は MAR で発生していないとダメ。サンプルデータとしては 再び employee_IQ_JP.csv を使う。
回帰には scikit-learn を使う。当たり前だが補間された値は回帰直線 (灰色破線) 上に乗る。
import sklearn.linear_model as lm reg = lm.LinearRegression() indexer = df['MAR'].isnull() reg.fit(df.loc[~indexer, ['IQ']], df.loc[~indexer, 'MAR']) predicted = reg.predict(df.loc[indexer, ['IQ']]) df.loc[indexer, 'MAR'] = predicted # プロット ax = df[indexer].plot.scatter(x='IQ', y='MAR', marker='^', color='red', label='missing'); ax = df[~indexer].plot.scatter(x='IQ', y='MAR', ax=ax); x = np.linspace(*ax.get_xlim()) ax.plot(x, reg.coef_[0] * x + reg.intercept_, color='gray', linestyle='dashed')

外れ値
外れ値をみるにはまずデータの分布 / 箱ヒゲ図を描くのがかんたん。
iris.plot(kind='hist', bins=50, subplots=True);
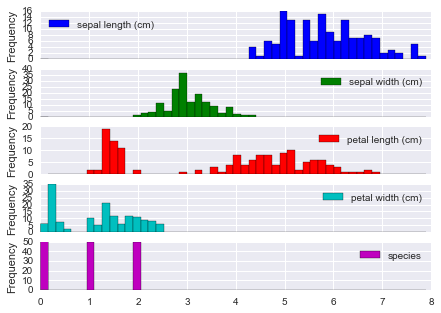
四分位範囲での検出
seaborn.boxplot では 外れ値はダイヤ "♦︎" で描画される。外れ値とみなす閾値は whis オプションを利用して指定できる。既定は 1.5 で、四分位範囲 (IQR) = 第3四分位 - 第1四分位 の 1.5 倍を超えるレコードが外れ値となる。
ここでは "species" のラベルごとに、各変数の箱ヒゲ図を描く。
fig, axes = plt.subplots(3, 1) for i, (n, g) in enumerate(iris.groupby('species')): sns.boxplot(data=g.iloc[:, :4], ax=axes[i]) axes[i].set_ylabel(n)

「データ分析プロセス」に記載されているその他の方法のうち、LOF (Local Outlier Factor) には Python のパッケージがあるが、メンテされているか謎だ。
また、scikit-learn の 1 クラス SVM や ガウス過程 を使う方法もある。これらは 機械学習プロフェッショナルシリーズ「状態変化と異常検知」に記載がある。

- 作者: 井手剛,杉山将
- 出版社/メーカー: 講談社
- 発売日: 2015/08/08
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (1件) を見る
離散化
以下 2 つの方法については pandas でできる。
| 方法 | 概要 |
|---|---|
| 等間隔区間 (EWD) | 対象のカラムの値を等間隔の区分で分割する |
| 等頻度区間 (EFD) | 分割した区分に同程度の数のレコードが含まれるように分割する |
等間隔区間による離散化
等間隔区間による離散化は pd.cut。どのように分割されたかは categories として表示される。
pd.cut(iris['sepal length (cm)'], 5) # 0 (5.02, 5.74] # 1 (4.296, 5.02] # ... # 148 (5.74, 6.46] # 149 (5.74, 6.46] # Name: sepal length (cm), dtype: category # Categories (5, object): [(4.296, 5.02] < (5.02, 5.74] < (5.74, 6.46] < (6.46, 7.18] < (7.18, 7.9]]
区分ごとのレコード数を数えるには Series.value_counts。結果を Series.sort_index して区分の順番に並べている。
pd.cut(iris['sepal length (cm)'], 5).value_counts().sort_index() # (4.296, 5.02] 32 # (5.02, 5.74] 41 # (5.74, 6.46] 42 # (6.46, 7.18] 24 # (7.18, 7.9] 11 # dtype: int64
等頻度区間による離散化
等頻度区間による離散化は pd.qcut。
pd.qcut(iris['sepal length (cm)'], 5) # 0 (5, 5.6] # 1 [4.3, 5] # ... # 148 (6.1, 6.52] # 149 (5.6, 6.1] # Name: sepal length (cm), dtype: category # Categories (5, object): [[4.3, 5] < (5, 5.6] < (5.6, 6.1] < (6.1, 6.52] < (6.52, 7.9]] pd.qcut(iris['sepal length (cm)'], 5).value_counts().sort_index() # [4.3, 5] 32 # (5, 5.6] 33 # (5.6, 6.1] 30 # (6.1, 6.52] 25 # (6.52, 7.9] 30 # dtype: int64
「データ分析プロセス」に記載されているその他の方法のうち、最小記述長原理 (MDLP) での離散化は scikit-learn に PR が上がっている。
| 方法 | Python パッケージ / リンク |
|---|---|
| 最小記述長原理 (MDLP) | Discretization using Fayyad's MDLP stop criterion by hlin117 · Pull Request #4801 · scikit-learn/scikit-learn · GitHub |
まとめ
書籍「データ分析プロセス」の流れに沿って、欠損値/外れ値/離散化の処理を、pandas で行う方法を記載した。
上で記載した方法 = Python でできる方法は書籍の内容のうち比較的 簡単な方法だけだ。より網羅的に知りたい方は書籍を読んでいただくのがいい。R ユーザに限らずおすすめ。

- 作者: 福島真太朗,金明哲
- 出版社/メーカー: 共立出版
- 発売日: 2015/06/25
- メディア: 単行本
- この商品を含むブログ (2件) を見る
Python Dask で Out-Of-Core / 並列 LU 分解
はじめに
正方行列 を
となる下三角行列
と 上三角行列
に分解することを LU 分解という。LU 分解ができると連立方程式の解や逆行列が 前進/後退代入でかんたんに求められてうれしい。
Dask を使って LU 分解を Out-Of-Core / 並列でやりたい。
LU 分解の並列化にはいくつかやり方があるようで、東大講義 スパコンプログラミング(1)、スパコンプログラミング(I) の 第10回 LU分解法 にまとまっている。この講義、ガイダンス資料の単位取得状況を見るとかなり楽しそうな感じだ。
ここでは、Dask での実装がかんたんそうなブロック形式ガウス法 (資料 P33-) をやりたい。
ブロック形式ガウス法
ブロック形式ガウス法では入力となる行列をいくつかのブロックに区切り、ブロックごとに処理を行う。具体的には、左上の対角ブロックからはじめて、以下の順番で処理していく。
- 対角ブロックの計算
- 1と同じ行のブロックの計算
- 1と同じ列のブロックの計算
- 一つ右下の対角ブロックへ
処理の順序を図示すると以下のような形。行/列の処理 (2, 3) は順序関係ないため入れ替えてもよい = 並列に処理できる。
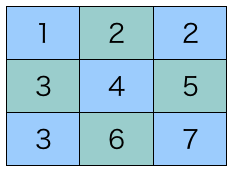
ブロック内の計算は 通常の (ブロック化しない) LU 分解や、基本的な行列演算の組み合わせで書ける。
上の PDF 資料では 3 ブロック目以降の式がよくわからないため、 行
列目のブロックを
として計算式を書いておく。
Python での実装を考慮して、逆行列ではなく scipy.linalg.solve (実際に使うのは solve_triangular ) を使って書く。
1. 対角ブロックの計算
※ は LU 分解を行う関数。
2. 1 と同じ行のブロックの計算
より、
※ は
を
について解く関数。
3. 1 と同じ列のブロックの計算
より、
Python での確認
具体的な処理を確かめるため、まず np.ndarray を手動でブロックに区切り、各ステップの計算を行う。
import numpy as np import scipy import scipy.linalg np.__version__ # '1.10.2' # 表示を丸め np.set_printoptions(precision=2) scipy.__version__ # '0.16.1'
LU 分解する行列 は以下のようなものにした。ブロックの大きさを 3 x 3 にした時、計 9 個のブロックができる。
A = np.array([[ 9., 3., 7., 8., 8., 10., 3., 8., 6.], [ 2., 10., 10., 1., 8., 3., 7., 4., 8.], [ 7., 8., 1., 5., 7., 9., 5., 9., 2.], [ 1., 8., 6., 6., 10., 7., 7., 9., 3.], [ 8., 8., 10., 9., 5., 3., 7., 5., 4.], [ 1., 4., 3., 4., 3., 10., 3., 2., 1.], [ 4., 1., 6., 5., 4., 9., 10., 6., 9.], [ 6., 9., 2., 3., 8., 1., 9., 4., 2.], [ 8., 6., 2., 9., 8., 9., 3., 10., 8.]]) A

まずは ブロック化せずに LU 分解の結果を確かめる。LU 分解は scipy.linalg.lu で行うことができ、返り値は P, L, U の 3 つの ndarray となる。
P は置換行列で、LU 分解時のピボット (行の入れ替え) 処理に対応する。今回は P が単位行列になっているため、ピボットなしで分解できていることがわかる。
P, L, U = scipy.linalg.lu(A) P
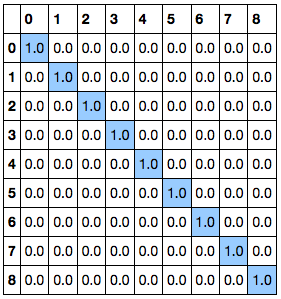
L, U
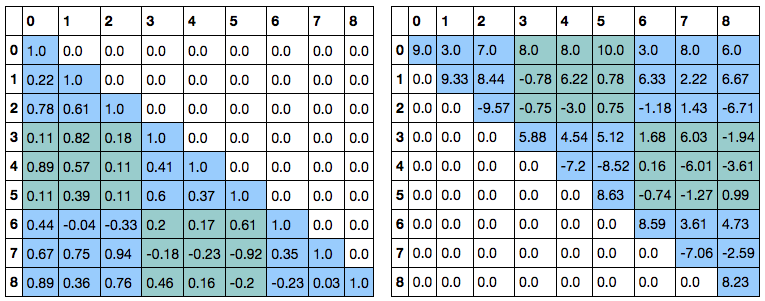
1. 対角ブロックの計算
まず、ndarray から i 行 j 列目のブロックを取り出す関数 block_slice を定義する。
def block_slice(m, i, j, size=3): return m[i*size:(i+1)*size, j*size:(j+1)*size] # 0 行 0 列目 A00 = block_slice(A, 0, 0) A00 # array([[ 9., 3., 7.], # [ 2., 10., 10.], # [ 7., 8., 1.]])
左上のブロック はそのまま LU 分解すればよい。LU 分解には
scipy.linalg.lu を使う。1 番目の返り値である P は単位行列となるため無視する。
_, L00, U00 = scipy.linalg.lu(A00) L00 # array([[ 1. , 0. , 0. ], # [ 0.22, 1. , 0. ], # [ 0.78, 0.61, 1. ]]) # 結果が一致するか確認。以降の出力は適宜省略 assert np.allclose(L00, block_slice(L, 0, 0)) assert np.allclose(U00, block_slice(U, 0, 0))
2. 1 と同じ行のブロックの計算
0 行目ならびに 0 列目では 上式の総和にあたる部分がないため、単に ,
を解けばよい。
は下三角行列であることから
scipy.linalg.solve_triangular で解ける。
# 0 行 1 列目 A01 = block_slice(A, 0, 1) U01 = scipy.linalg.solve_triangular(L00, A01, lower=True) U01 # array([[ 8. , 8. , 10. ], # [ -0.78, 6.22, 0.78], # [ -0.75, -3. , 0.75]]) # 0 行 2 列目 A02 = block_slice(A, 0, 2) U02 = scipy.linalg.solve_triangular(L00, A02, lower=True) assert np.allclose(U01, block_slice(U, 0, 1)) assert np.allclose(U02, block_slice(U, 0, 2))
3. 1 と同じ列のブロックの計算
こちらも上式そのまま。
# 1 行 0 列目 A10 = block_slice(A, 1, 0) L10 = scipy.linalg.solve_triangular(U00.T, A10.T, lower=True).T L10 # array([[ 0.11, 0.82, 0.18], # [ 0.89, 0.57, 0.11], # [ 0.11, 0.39, 0.11]]) # 2 行 0 列目 A20 = block_slice(A, 2, 0) L20 = scipy.linalg.solve_triangular(U00.T, A20.T, lower=True).T assert np.allclose(L10, block_slice(L, 1, 0)) assert np.allclose(L20, block_slice(L, 2, 0))
4. 一つ右下の対角ブロックへ
# 1 行 1 列目 A11 = block_slice(A, 1, 1) _, L11, U11 = scipy.linalg.lu(A11 - L10.dot(U01)) L11 # array([[ 1. , 0. , 0. ], # [ 0.41, 1. , 0. ], # [ 0.6 , 0.37, 1. ]]) assert np.allclose(L11, block_slice(L, 1, 1)) assert np.allclose(U11, block_slice(U, 1, 1))
以降、上式と同じ処理を続ける。
# 1 行 2 列目 A12 = block_slice(A, 1, 2) U12 = scipy.linalg.solve_triangular(L11, A12 - L10.dot(U02), lower=True) assert np.allclose(U12, block_slice(U, 1, 2)) # 2 行 1 列目 A21 = block_slice(A, 2, 1) L21 = scipy.linalg.solve_triangular(U11.T, (A21 - L20.dot(U01)).T, lower=True).T assert np.allclose(L21, block_slice(L, 2, 1)) # 2 行 2 列目 A22 = block_slice(A, 2, 2) _, L22, U22 = scipy.linalg.lu(A22 - L20.dot(U02) - L21.dot(U12)) L22 # array([[ 1. , 0. , 0. ], # [ 0.35, 1. , 0. ], # [-0.23, 0.03, 1. ]]) assert np.allclose(L22, block_slice(L, 2, 2)) assert np.allclose(U22, block_slice(U, 2, 2))
ここまでで、ブロック形式ガウス法の具体的な処理が確かめられた。
置換行列 P の処理
P は行の入れ替えに対応するので、"2. 対角ブロックと同じ行のブロックの計算" を行う前後で P を考慮した変換をすればよい。置換行列の逆行列は転置と一致する ( ) ため、
inv や solve は不要。
Dask での実装
Dask では計算処理を以下のような DAG で定義する。定義したグラフは Dask のスケジューラによって自動的に Out-Of-Core / 並列処理される。ブロック形式ガウス法では行/列の処理 (2, 3) や、各ブロック内での計算中に出てくる行列積は 順序関係ないため並列で実行できる。
上の処理を Dask のグラフとして書き直すと以下のようになる。置換行列 P の処理も追加している。
# 利用するには1/23以降のmaster (公式には 0.7.6 の次のバージョン) が必要 dA = da.from_array(A, (3, 3)) dP, dL, dU = da.linalg.lu(dA) assert np.allclose(dL.compute(), L) assert np.allclose(dU.compute(), U) # 結果は上と同一のため略 dL.visualize()
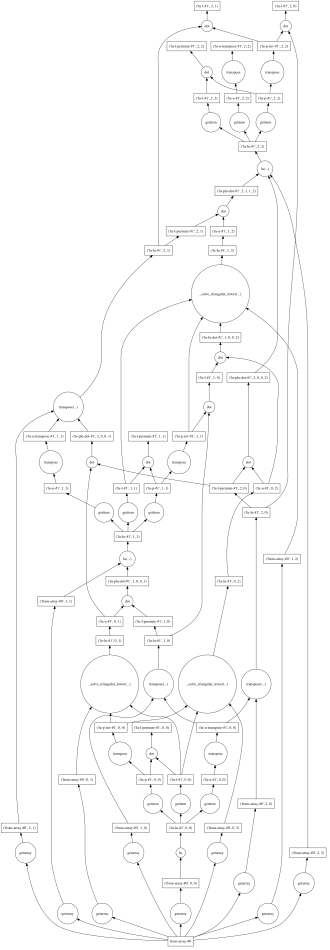
まとめ
ブロック形式ガウス法の処理方法を確認し、Dask での実装を行った。LU 分解の結果を利用すると、連立方程式の解や逆行列も Out-Of-Core / 並列で求めることができる。
- ENH: add da.linalg.solve by sinhrks · Pull Request #938 · blaze/dask · GitHub
- ENH: add da.linalg.inv by sinhrks · Pull Request #939 · blaze/dask · GitHub

- 作者: 片桐孝洋
- 出版社/メーカー: 東京大学出版会
- 発売日: 2013/03/13
- メディア: 単行本
- この商品を含むブログを見る
Cesium.js を Python から使うパッケージを作った
3D 地図を表示する JavaScript ライブラリである Cesium.js を Python から簡単に使いたい。Cesium.js についてはこちらを。
上に記載した方法は、可視化したい内容に応じて JavaScript のテンプレートを作成し、Python からデータを埋め込むというものだった。が、都度 テンプレートを作るのはさっと可視化したい場合にはめんどくさい。
ということでこれを Python のみ / JavaScript なしで利用できるパッケージを書いた。
使い方
サンプルデータは前と同じく こちらのエントリのものを利用する。作成した DataFrame は変数 df に入っているとする。
インストール
pip で。
$ pip install cesiumpy
地図の表示
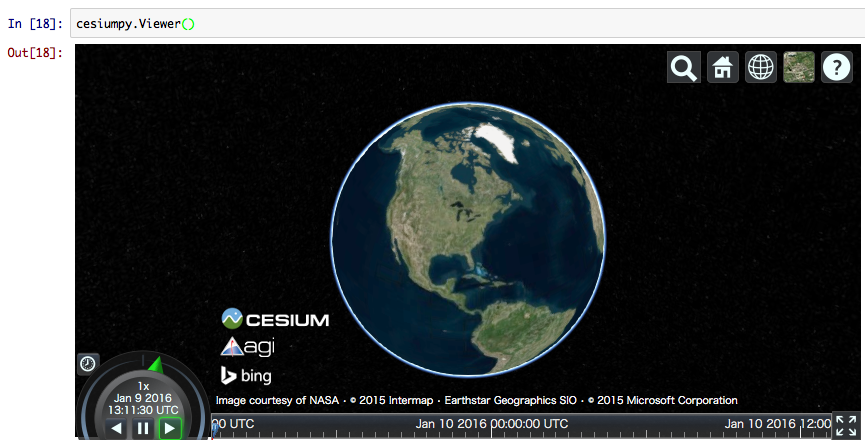
以降の操作は Jupyter Notebook 上で行う。装飾のない地図を表示したいだけなら Viewer インスタンスを作成すればよい。地図は Jupyter のセルに埋め込まれて表示される。
import cesiumpy cesiumpy.__version__ # '0.1.1' cesiumpy.Viewer()
グラフの描画
Cesium.js では以下のような図形 ( Entity ) が描画できる。cesiumpy を使うとこれらを Python のみで作成 / 描画できる。
PointLabelBoxEllipseCylinderPolygonRectangleEllipsoidWallCorridorPolylinePolylineVolumeBillboard
ここではそのうちいくつかを例として記載する。ドキュメントには全ての Entity の画像と作り方を簡単に記載している。
Cylinder
上の例と同じく、Cylinder で 3D 棒グラフを描く。Entity を描画するには、まず当該のインスタンスを作成し、Viewer.entities.add メソッドに渡せばよい。
v = cesiumpy.Viewer() for i, row in df.iterrows(): l = row['Recreation Visitors (2014)[5]'] cyl = cesiumpy.Cylinder(position=[row['lon'], row['lat'], l / 2.], length=l, topRadius=10e4, bottomRadius=10e4, material='aqua') v.entities.add(cyl) v
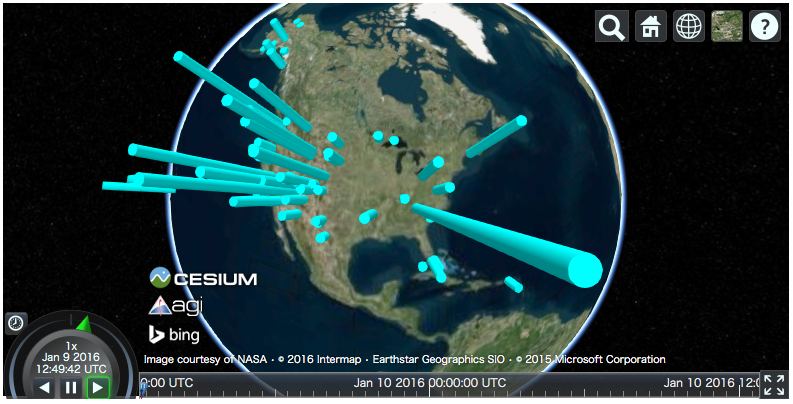
Point
Point クラスを使うと バブルチャートが描ける。
また、右上に並んだアイコンで投影法や地面の画像 ( Imagery ) が変更できる。ここでは Open Street Map を表示している。Imagery は スクリプトからも変更できる。
v = cesiumpy.Viewer() for i, row in df.iterrows(): l = row['Recreation Visitors (2014)[5]'] p = cesiumpy.Point(position=[row['lon'], row['lat'], 0], pixelSize=np.sqrt(l / 10000), color='blue') v.entities.add(p) v

Billboard ( Pin )
Leaflet のように ピン を表示する場合は Billboard と Pin を使う。ピンの色やラベルを変更することもできる。
v = cesiumpy.Viewer() pin = cesiumpy.Pin() for i, row in df.iterrows(): l = row['Recreation Visitors (2014)[5]'] b = cesiumpy.Billboard(position=[row['lon'], row['lat'], 0], image=pin, scale=0.4) v.entities.add(b) v

scipy.spatial の利用
また、cesiumpy は scipy.spatial に含まれる以下のような図を地図上に重ねて描くことができる。
- ボロノイ図 (
scipy.spatial.Voronoi) - 凸包 (
scipy.spatial.ConvexHull)
まずはデータを合衆国本土のみにフィルタする。
filtered = df[(-130 < df['lon']) & (df['lon'] < -60) & (20 < df['lat']) & (df['lat'] < 50)] filtered.shape # (47, 10)
フィルタしたデータから、各レコードの座標 (経度, 緯度) からなる tuple の list を作成する。
pos = filtered[['lon', 'lat']].values pos = [tuple(p) for p in pos] pos # [(-68.129999999999995, 44.210000000000001), # (-109.34, 38.409999999999997), # ... # (-119.3, 37.5), # (-113.03, 37.18)]
まず scipy で書くとこのような処理になる。詳細は以下のドキュメントに記載されているが、プロットの見た目を変更したり、各領域の座標を再利用できる形に変換するのは少し手間だ。
- scipy.spatial.Voronoi — SciPy v0.16.1 Reference Guide
- Spatial data structures and algorithms (scipy.spatial) — SciPy v0.16.1 Reference Guide
from scipy.spatial import Voronoi, voronoi_plot_2d vor = Voronoi(pos) vor # <scipy.spatial.qhull.Voronoi at 0x107dbab50> voronoi_plot_2d(vor)

一方、cesiumpy でやるとこんな感じ。cesiumpy.spatial.Voronoi.get_polygons() は、各座標を 対応するボロノイ領域を含む Polygon のリストに変換する。これに適当に色付けして地図上に表示すればよい。
ボロノイ領域は元の座標と同じ順序になっているため、元座標に応じて色分けすることもできる。
colors = [cesiumpy.color.BLUE, cesiumpy.color.RED, cesiumpy.color.YELLOW, cesiumpy.color.ORANGE,
cesiumpy.color.PURPLE, cesiumpy.color.GREEN, cesiumpy.color.WHITE, cesiumpy.color.AQUA,
cesiumpy.color.NAVY, cesiumpy.color.PINK, cesiumpy.color.MAGENTA]
v = cesiumpy.Viewer()
polygons = cesiumpy.spatial.Voronoi(pos).get_polygons()
colors = np.random.choice(colors, len(polygons))
for p, c in zip(polygons, colors):
p.material = c.set_alpha(0.1)
p.outline = True
v.entities.add(p)
v
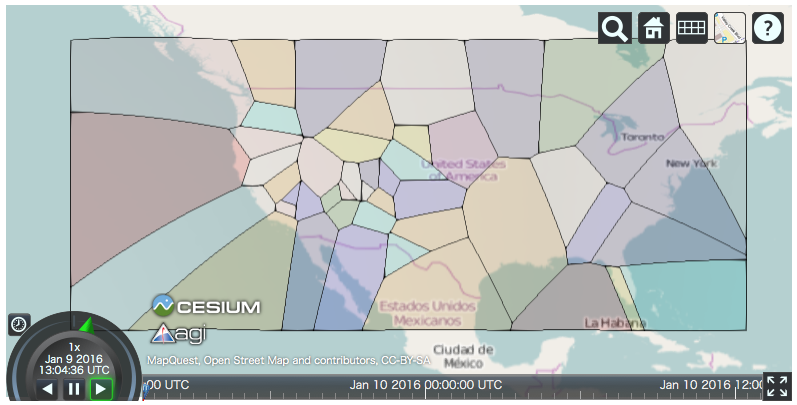
まとめ
cesiumpy を使うと Cesium.js を利用した可視化が JavaScript なしで書ける。
Entityを利用したグラフの描画、可視化- ボロノイ図や凸包の描画
また、上には含めなかったが下のような処理もできる。

インタラクティブ・データビジュアライゼーション ―D3.jsによるデータの可視化
- 作者: Scott Murray,長尾高弘
- 出版社/メーカー: オライリージャパン
- 発売日: 2014/02/19
- メディア: 大型本
- この商品を含むブログ (3件) を見る
Python pandas で e-Stat のデータを取得したい
e-Stat とは
"「政府統計の総合窓口(e-Stat)」は、各府省が公表する統計データを一つにまとめ、統計データの検索をはじめとした、さまざまな機能を備えた政府統計のポータルサイト" だそうだ。このデータを pandas で読めるとうれしい...ということで対応した。
インストール
$ pip install japandas
パッケージのインポート
import numpy as np np.__version__ # '1.10.2' import pandas as pd pd.__version__ # u'0.17.1' import japandas as jpd jpd.__version__ # '0.2.0'
アプリケーション ID の取得
e-Stat を利用するには 利用登録とアプリケーション ID の取得が必要。利用ガイドに沿って登録する。
データの取得
japandas を利用してデータを取得する。データの取得は以下 2 ステップで行う
- "政府統計コード" を利用して、統計調査に含まれる統計表 ( 実データ ) の一覧とその ID ( 統計表 ID ) を取得する。
- 取得した統計表 ID を利用して、実データを取得する
1. 統計表一覧の取得
e-Stat 提供データ一覧 に含まれる統計調査のうち、今回は 00200564 全国消費実態調査 を利用する。
jpd.DataReader で ID "00200564" のデータを取得すると、以下のような DataFrame が返ってくる。各カラムの詳細は e-Stat API 仕様 に記載されている。
key = "Your application ID" dlist = jpd.DataReader("00200564", 'estat', appid=key) dlist

一つの "統計表題名及び表番号" は "調査年月" が異なる複数のデータを持つことがある。値をユニークにした方が中身を確認しやすい。
tables = dlist[u'統計表題名及び表番号'].value_counts().to_frame()
tables

ここでは "平成26年全国消費実態調査 > 全国 > 品目及び購入先・購入地域に関する結果 > 単身世帯" の "男女,年齢階級,購入形態,品目別1世帯当たり1か月間の支出" のデータを取得したい。
この時点では 正確な "統計表題名及び表番号" がわからないため、まずはそれらしい文字列でレコードを抽出する。
indexer = tables.index.str.contains(u'男女,年齢階級,購入形態,品目別1世帯当たり1か月間の支出') indexer # array([False, False, False, ..., False, False, False], dtype=bool) tables[indexer]

上の結果から 正確な "統計表題名及び表番号" が得られるため、元データから対象のレコードが抽出できる。
table = tables[indexer].index[0] table # [単身世帯]フロー編第149表 男女,年齢階級,購入形態,品目別1世帯当たり1か月間の支出 target = dlist[dlist[u'統計表題名及び表番号'] == table] target

2. 実データの取得
- で調べた "統計表 ID" (
"0003109612") をjpd.DataReaderに渡せばよい。
df = jpd.DataReader("0003109612", 'estat', appid=key) # 略
が、いちいち文字列を抽出したり再入力するのは面倒だ。そんな時は、上の結果 ( 取得対象の "統計表 ID" を含む DataFrame) をそのまま渡してもよい。複数のレコードがある場合は全データを連結して返す。
df = jpd.DataReader(target, 'estat', appid=key)
df

出典:「平成26年全国消費実態調査調査結果」(総務省統計局)
取得したデータを集計してみる。各属性に対応する値は "value" カラムに含まれている。まず、カラム名を簡潔なものに変更する。
df.columns =[u'value', u'世帯区分', u'品目分類表', u'地域', u'表章項目', u'男女', u'年齢階級', u'購入形態']
また、dtypes を見ると全ての列が object 型になっている。通常、"value" には数値が入るため、jpd.DataReader は "value" が数値に変換できる場合は自動で変換するのだが、このデータでは何らかの理由で失敗しているようだ。
df.dtypes # value object # 世帯区分 object # 品目分類表 object # 地域 object # 表章項目 object # 男女 object # 年齢階級 object # 購入形態 object # dtype: object
pd.to_numeric で数値に変換しようとすると ValueError が発生する。データを見ると "value" にハイフン "-" がいくつか使われているようだ (やめてくれ...)。
文字列処理してもよいが、今回は特に何もしなくても以降の処理で解決されるため、とりあえずそのままにしておく。
1/9 補足 v0.2.1 では "-" を欠損として扱うように修正済み。
pd.to_numeric(df['value']) # ValueError: Unable to parse string df['value'].str.isnumeric() # 時間軸(年次) # 2014-01-01 True # 2014-01-01 True # 2014-01-01 True # 2014-01-01 False # ... # 2014-01-01 False # 2014-01-01 False # 2014-01-01 False # 2014-01-01 False # Name: value, dtype: bool
"品目分類表" の値をみるとかなり細かい項目に分けられていることがわかる。
統計調査に利用された調査票 を参照すると、調査形式は家計簿のようなフォーマットに任意の品名を書き込むもののようだ。品目分類を被調査者が記入する欄はなく、集計時に家計簿を品目分類表に従って分類しているのだろう。
df[u'品目分類表'].unique() # array([u'集計世帯数', # u'世帯数分布(抽出率調整)', # u'世帯数分布(抽出率調整)(1万分比)', # ..., u'仕送り金', # u'国内遊学仕送り金', # u'他の仕送り金'], dtype=object)
データから "すし" を含むレコードを抽出してみる。...弁当とは? この調査票には詳細が記載されていないようだが、他の調査を見ると スーパーで買うパックの寿司を指しているものと思う (おにぎりは別項目)。
filtered = df[df[u'品目分類表'].str.contains(u'すし')] filtered

抽出されたレコードの
"value" には 数値として不正な文字列は含まれないため、pd.to_numeric で数値に変換できる。
filtered['value'] = pd.to_numeric(filtered['value']) filtered.dtypes # value int64 # 世帯区分 object # 品目分類表 object # 地域 object # 表章項目 object # 男女 object # 年齢階級 object # 購入形態 object # dtype: object
Series.nunique で各列に含まれるユニークな値の数を調べる。"男女", "年齢階級", "購入形態" でレコードが分かれているため、それら 3 つをキーにして集計してやればよい。
filtered.apply(lambda x: x.nunique()) # value 76 # 世帯区分 1 # 品目分類表 1 # 地域 1 # 表章項目 1 # 男女 3 # 年齢階級 8 # 購入形態 4 # dtype: int64 sushi = pd.pivot_table(filtered, index=[u'男女', u'年齢階級'], columns=u'購入形態', values='value', aggfunc='sum') sushi

"購入形態" (支払い方法) には興味がないので、"合計" の値だけを抽出してプロットする。
60 代 男性 単身者 は "すし(弁当)" への消費金額が比較的多いようだ。金額的に月 1 〜 2 回買っている感じだろうか。また女性も一部男性と比べ高い。
sushi = sushi[[u'合計']] sushi.plot.bar(ylim=(0, 1000))

追加データでの確認
同じ統計調査に "二人以上の世帯" のデータも含まれているので、同項目をみてみる。先ほどと同じように、まず 対象の統計表 ID を調べる。世帯別の集計になるため、男女/年齢といった区分はないが、品目別の支出がわかるデータを探す。
indexer2 = tables.index.str.contains(u'品目別1世帯当たり1か月間の支出') tables[indexer2]

table2 = tables[indexer2].index[3] target2 = dlist[dlist[u'統計表題名及び表番号'] == table2] target2

見つけた 統計表 ID から実データを取得する。
df2 = jpd.DataReader(target2, 'estat', appid=key)
df2

カラム名を変更し、"すし" かつ 地域が "全国" のデータのみを抽出する。
df2.columns = [u'value', u'世帯区分', u'品目分類表', u'地域', u'表章項目'] sushi2 = df2[df2[u'品目分類表'].str.contains(u'すし') & (df2[u'地域'] == u'全国')] sushi2[u'value'] = pd.to_numeric(sushi2[u'value']) sushi2

この数値が二人以上世帯での消費金額の平均になる。先のグラフに重ねてプロットする。
ax = sushi.sum(axis=1).plot.bar(ylim=(0, 1000)) ax.axhline(y=sushi2.iloc[1, 0], color='red')

単身者で 二人以上世帯の消費金額とほぼ同じ金額を使っていれば消費が多いと言ってよさそうだ。単純な見方をすると 料理は面倒だし外食は気疲れする...と感じる頻度が高い層が買っているのだろうか。被調査者によってかなり偏りがあると考えられるので、ここまで細項目を取るなら分布が見てみたい。

Pythonによるデータ分析入門 ―NumPy、pandasを使ったデータ処理
- 作者: Wes McKinney,小林儀匡,鈴木宏尚,瀬戸山雅人,滝口開資,野上大介
- 出版社/メーカー: オライリージャパン
- 発売日: 2013/12/26
- メディア: 大型本
- この商品を含むブログ (12件) を見る
Python Jupyter + Cesium.js で 3D 地図が描きたい
Cesium.js とは
Web GL を利用して 3D 地図を描画する JavaScript ライブラリ。かなり多機能で様々な見せ方ができるようだ。詳しく知りたい方は公式サイトの Demos を見ればいい。
これを Jupyter Notebook に埋め込んで使いたい。Cesium.js には Python の wrapper などはないため、直接 JavaScript を書いて使う。従って、利用できる機能に差異はない。このエントリでは Cesium.js の機能の詳細には触れず、Jupyter に関係する内容のみ記載する。
具体的なやり方はこちらと同じ。
データの準備
先日のエントリで作成した、 アメリカの国立公園 のデータを使う。
以降、すべて Jupyter Notebook 上で行う。先のエントリで処理済みのデータは df 変数に入っているとする。
import numpy as np np.__version__ # '1.10.2' import pandas as pd pd.__version__ # u'0.17.1' df # 略
Cesium.js の利用
まずは必要な JavaScript と CSS を読み込む。
2016/01/05 CSS のパスが誤っていたため修正
%%html <script src="https://cesiumjs.org/Cesium/Build/Cesium/Cesium.js"></script> <link rel="stylesheet" href="http://cesiumjs.org/Cesium/Build/Cesium/Widgets/widgets.css" type="text/css">
Jupyter 上に HTML を直接 書いて、 Cesium.js がロードできるか確かめる。うまくいっていれば以下のような全球地図が表示され、インタラクティブに操作ができる。
%%html <div id="container1" style="width:100%; height:100%;"></div> <script type="text/javascript"> var widget = new Cesium.CesiumWidget('container1'); </script>

Cesium 上に何かを描画する場合は Viewer クラスを使うのが良いようだ。 Viewer は上で利用した CesiumWidget クラスに加え、画面をコントロールするための多くのメニューを持つ。各メニューの表示 / 非表示はオプションで切り替えられる。それぞれの意味は以下のドキュメントを。
ここでは、以下の2つを除いて無効にした (既定では有効)。
animation: 画面左下、製造元リンクがsceneModePickerに被らないようにするために有効化sceneModePicker: 地図の投影方式を選択するために有効化
options = dict(animation=True, baseLayerPicker=False, fullscreenButton=False, geocoder=False, homeButton=False, infoBox=False, sceneModePicker=True, selectionIndicator=False, navigationHelpButton=False, timeline=False, navigationInstructionsInitiallyVisible=False) import json json.dumps(options) # '{"geocoder": false, "fullscreenButton": false, "timeline": false, # "baseLayerPicker": false, "sceneModePicker": true, "navigationHelpButton": false, # "infoBox": false, "animation": true, "homeButton": false, "selectionIndicator": false, # "navigationInstructionsInitiallyVisible": false}' template = """ <div id="{container}" style="width:90%; height:90%;"></div> <script type="text/javascript"> var viewer = new Cesium.Viewer('{container}', {options}); {script} </script> """ t = template.format(container='container2', options=json.dumps(options), script='') from IPython.display import HTML HTML(t)

この地図上に 3D 棒グラフを描きたい。
まず、円柱 ( cylinder ) を一つだけ描画してみる。描画する位置は Cesium.Cartesian3.fromDegrees で指定する。この座標は 地面 (円柱底面) ではなく 円柱中央の座標のため、円柱の長さに合わせて位置を調整する必要がある。具体的には、Cartesian3.fromDegreesの 3 要素目 ( center ) を長さ ( length ) の 1/2 とすればよい。
script = """ viewer.entities.add({{ name : 'Cylinder', position: Cesium.Cartesian3.fromDegrees({lon}, {lat}, {center}), cylinder : {{ length : {length}, topRadius : 100000, bottomRadius : 100000, material : Cesium.Color.AQUA.withAlpha(0.5), }} }});""" t = template.format(container='container3', options=json.dumps(options), script=script.format(lon=-110, lat=50, length=4000000, center=2000000)) HTML(t)
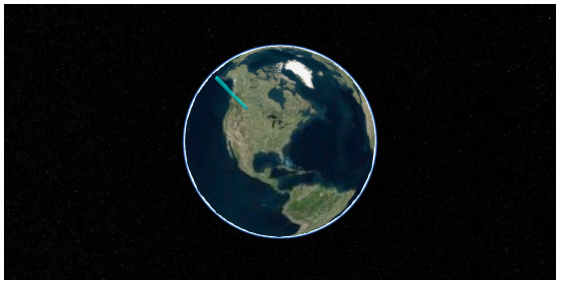
うまくいっているようだ。地図の回転、拡大縮小に円柱も追従している。
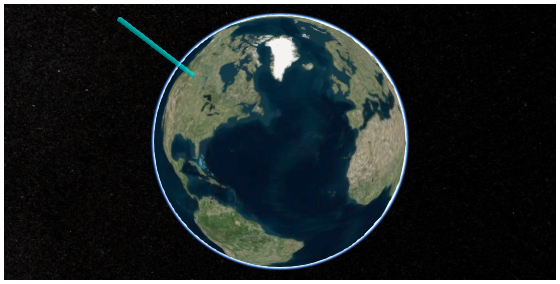
3D 棒グラフを描くには 上の処理をレコード数分繰り返せばよい。先日と同じく、各国立公園の 2014 年の入園者数を円柱の長さとしてプロットする。
scripts = [] for i, row in df.iterrows(): l = row['Recreation Visitors (2014)[5]'] scripts.append(script.format(lat=row['lat'], lon=row['lon'], length=l, center=l / 2.)) scripts = ''.join(scripts) t = template.format(container='container4', options=json.dumps(options), script=scripts) HTML(t)
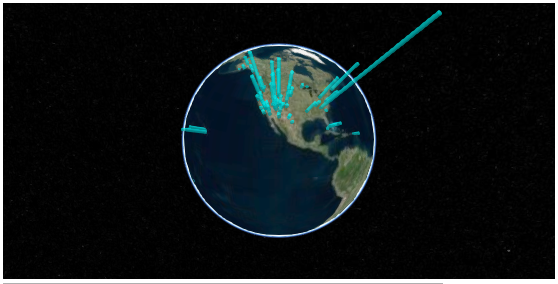
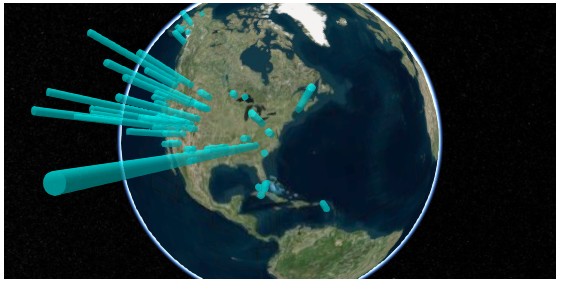
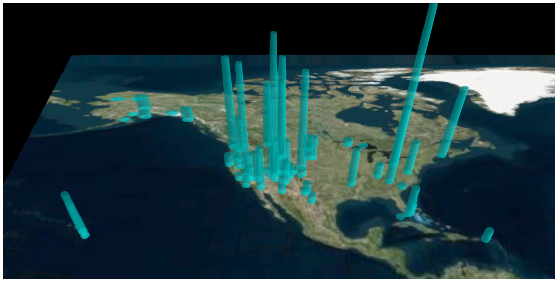
sceneModePicker のアイコンをクリックすると、平面上に地図が投影される。
まとめ
Jupyter Notebook 上に Cesium.js の 3D 地図を埋め込む方法を記載した。また、埋め込んだ地図上に Python で準備したデータを使って オブジェクトを追加した。
Cesium.js、触っていて楽しいし、少し面白い見せ方をしたい時に使えそうだ。
2016/01/21追記 パッケージを書いた

インタラクティブ・データビジュアライゼーション ―D3.jsによるデータの可視化
- 作者: Scott Murray,長尾高弘
- 出版社/メーカー: オライリージャパン
- 発売日: 2014/02/19
- メディア: 大型本
- この商品を含むブログ (3件) を見る
Python pandas + folium で Leaflet をもっと使いたい
先日参加させていただいた Japan.R でこんな話を聞いた。
Python でも folium というパッケージを使うと JavaScript を書かなくても Leaflet.js の一部機能が使えるのだがあまり情報がない。上の資料に書いてあるようなことが folium でもできるのか調べたい。
folium については前にこんなエントリを書いた。
データの準備
import numpy as np np.__version__ # '1.10.2' import pandas as pd pd.__version__ # u'0.17.1'
サンプルデータとして Wikipedia にある アメリカの国立公園 のデータを使う。まずは pd.read_html でデータを読みこむ。
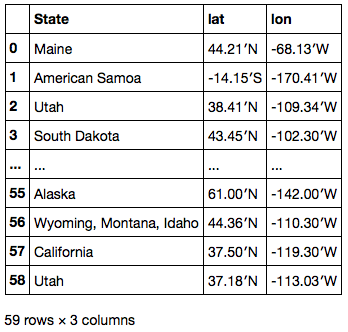
url = "https://en.wikipedia.org/wiki/List_of_national_parks_of_the_United_States" df = pd.read_html(url, header=0)[0] df

位置情報は "Location" カラムに文字列として保存されている。これを文字列処理して緯度・経度 別々の数値列に変換する。
df['Location'] # 0 Maine 44°21′N 68°13′W<feff> / <feff>44.35°N 68.21°W<feff> / 4... # 1 American Samoa 14°15′S 170°41′W<feff> / <feff>14.25°S 17... # 2 Utah 38°41′N 109°34′W<feff> / <feff>38.68°N 109.57°W<feff> / ... # 3 South Dakota 43°45′N 102°30′W<feff> / <feff>43.75°N 102.... # ... # 55 Alaska 61°00′N 142°00′W<feff> / <feff>61.00°N 142.00°W<feff> ... # 56 Wyoming, Montana, Idaho 44°36′N 110°30′W<feff> / <feff>4... # 57 California 37°50′N 119°30′W<feff> / <feff>37.83°N 119.50... # 58 Utah 37°18′N 113°03′W<feff> / <feff>37.30°N 113.05°W<feff> / ... # Name: Location, dtype: object
まずは .str.extract で Series 中の各要素から正規表現にマッチしたグループを取り出し、州名、緯度、経度 3 列の DataFrame に展開する。
locations = df['Location'].str.extract(u'(\D+) (\d+°\d+′[NS]) (\d+°\d+′[WE]).*') locations.columns = ['State', 'lat', 'lon'] locations
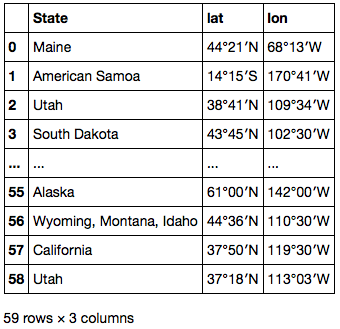
数値としてパースできるよう、.str.replace で記号を置換する。また、南半球 / 西半球の場合は緯度経度を負とするためマイナス符号をつけておく。
locations['lat'] = locations['lat'].str.replace(u'°', '.') locations['lon'] = locations['lon'].str.replace(u'°', '.') locations.loc[locations['lat'].str.endswith('S'), 'lat'] = '-' + locations['lat'] locations.loc[locations['lon'].str.endswith('W'), 'lon'] = '-' + locations['lon'] locations
最後の 2 文字は不要のため、.str.slice_replace を使って削除する ( None と置換する )。これで float64 型に変換できるようになる。
locations['lat'] = locations['lat'].str.slice_replace(start=-2) locations['lon'] = locations['lon'].str.slice_replace(start=-2) locations[['lat', 'lon']] = locations[['lat', 'lon']].astype(float) locations

処理した DataFrame を pd.concat で元の DataFrame に追加する。
locations.dtypes # State object # lat float64 # lon float64 # dtype: object df = pd.concat([df, locations], axis=1)
地図の描画
folium で描画した地図は Jupyter Notebook に埋め込んで利用したい。Jupyter 上に描画するための関数を定義する。
import folium folium.__version__ # '0.1.6' from IPython.display import HTML def inline_map(m): m._build_map() iframe = '<iframe srcdoc=\"{srcdoc}\" style=\"width: 80%; height: 400px; border: none\"></iframe>' return HTML(iframe.format(srcdoc=m.HTML.replace('\"', '"')))
まずは シンプルなマーカー。これは前のエントリでやったことと同じ。
m = folium.Map(location=[55, -108], zoom_start=3.0) for i, row in df.iterrows(): m.simple_marker([row['lat'], row['lon']], popup=row['Name']) inline_map(m)

マーカーをクラスタとして表示するには、clustered_marker キーワードに True を渡すだけ。
m = folium.Map(location=[55, -108], zoom_start=3.0) for i, row in df.iterrows(): m.simple_marker([row['lat'], row['lon']], popup=row['Name'], clustered_marker=True) inline_map(m)

地図を拡大・縮小するとマーカーのクラスタ表示が適当に切り替わる。

サークルを表示するには circle_marker を使う。各国立公園の 2014 年の入園者数をサークルの大きさとしてプロットする。
m = folium.Map(location=[40, -95], zoom_start=4.0) for i, row in df.iterrows(): m.circle_marker([row['lat'], row['lon']], radius=np.sqrt(row['Recreation Visitors (2014)[5]']) * 100, popup=row['Name'], line_color='#DF5464', fill_color='#EDA098', fill_opacity=0.5) inline_map(m)

ポリラインは line で引ける。引数には、各点の緯度と経度からなるリストのリストを渡せばよい。グランドキャニオンからいくつかの国立公園を結ぶポリラインを描画してみる。
dests = ['Grand Canyon', 'Zion', 'Bryce Canyon', 'Capitol Reef', 'Arches'] loc_df = df.set_index('Name') locations = loc_df.loc[dests, ['lat', 'lon']].values.tolist() locations # [[36.04, -112.08], # [37.18, -113.03], # [37.34, -112.11], # [38.12, -111.1], # [38.41, -109.34]] m = folium.Map(location=[37.5, -111], zoom_start=7.0) m.line(locations=locations) for dest, loc in zip(dests, locations): m.simple_marker(loc, popup=dest) inline_map(m)

Google Maps Direction API の利用
2 点間の経路をポリラインで描画したい、といった場合は 上のやり方 / 現在のデータでは無理だ。Google Maps Direction API を使って取得した 2 点間の経路をポリラインとして描きたい。
Google Maps Direction API へのアクセスには googlemaps パッケージを利用する。インストールは pip でできる。
ドキュメントはなく、使い方はテストスクリプトを見ろ、とだいぶ硬派な感じだ。それでも自分で API 仕様を調べるよりは早いと思う。
import googlemaps googlemaps.__version__ # '2.4.2'
googlemaps は Google Map に関連したいくつかの API をサポートしている。Directions API を使うには Client.directions。 mode として渡せるのは "driving", "walking", "bicycling", "transit" いずれか。
key = "Your application key" client = googlemaps.Client(key) result = client.directions('Grand Canyon, AZ, USA', 'Arches, UT, USA', mode="driving", departure_time=pd.Timestamp.now()) import pprint pprint.pprint(result, depth=5) # [{u'bounds': {u'northeast': {u'lat': 38.6164979, u'lng': -109.336915}, # u'southwest': {u'lat': 35.8549308, u'lng': -112.1400703}}, # u'copyrights': u'Map data \xa92015 Google', # u'legs': [{u'distance': {u'text': u'333 mi', u'value': 535676}, # u'duration': {u'text': u'5 hours 36 mins', u'value': 20134}, # u'duration_in_traffic': {u'text': u'5 hours 31 mins', # u'value': 19847}, # u'end_address': u'Arches National Park, Utah 84532, USA', # u'end_location': {u'lat': 38.6164979, u'lng': -109.6157153}, # u'start_address': u'Grand Canyon Village, AZ 86023, USA', # u'start_location': {u'lat': 36.0542422, u'lng': -112.1400703}, # u'steps': [{...}, # ...
結果は経路上のポイントごとに step として含まれるようだ。各ステップ の end_location を取得して地図上にプロットすると、ざっくりとした経路がわかる。
steps = result[0]['legs'][0]['steps'] steps[:2] # [{u'distance': {u'text': u'344 ft', u'value': 105}, # u'duration': {u'text': u'1 min', u'value': 10}, # u'end_location': {u'lat': 36.054091, u'lng': -112.1412252}, # u'html_instructions': u'Head <b>west</b>', # u'polyline': {u'points': u'_z`{EljmkT\\fF'}, # u'start_location': {u'lat': 36.0542422, u'lng': -112.1400703}, # u'travel_mode': u'DRIVING'}, # {u'distance': {u'text': u'141 ft', u'value': 43}, # u'duration': {u'text': u'1 min', u'value': 8}, # u'end_location': {u'lat': 36.0544236, u'lng': -112.1414507}, # u'html_instructions': u'Turn <b>right</b> toward <b>Village Loop Drive</b>', # u'maneuver': u'turn-right', # u'polyline': {u'points': u'ay`{EtqmkTI@GBGBIDGFIDKL'}, # u'start_location': {u'lat': 36.054091, u'lng': -112.1412252}, # u'travel_mode': u'DRIVING'}] locs = [step['end_location'] for step in steps] locs = [[loc['lat'], loc['lng']] for loc in locs] locs # [[36.054091, -112.1412252], # [36.0544236, -112.1414507], # [36.05547, -112.1384223], # [36.0395224, -112.1216684], # [36.0520635, -112.1055832], # [35.8550626, -111.4251481], # [36.0755773, -111.3918428], # [36.9304583, -109.5745837], # [37.2655159, -109.6257182], # [37.6254146, -109.4780126], # [37.6254311, -109.4754401], # [38.5724833, -109.5507785], # [38.6109465, -109.6081511], # [38.6164979, -109.6157153]] m = folium.Map(location=[37.5, -111], zoom_start=7.0) m.line(locations=locs) m.simple_marker(locs[0], popup='Grand Canyon, AZ, USA') m.simple_marker(locs[-1], popup='Arches, UT, USA') inline_map(m)

各ステップ中のより詳細な座標は polyline 中に Encoded Polyline Algorithm Format で記録されている。これは googlemaps.convert.decode_polyline 関数でデコードできる。
steps[0]['polyline'] # {u'points': u'_z`{EljmkT\\fF'} googlemaps.convert.decode_polyline(steps[0]['polyline']['points']) # [{'lat': 36.05424, 'lng': -112.14007000000001}, # {'lat': 36.05409, 'lng': -112.14123000000001}]
全ての step から polyline 中の座標を取得すればよさそうだ。適当な関数を書いて地図上にプロットする。
def get_polylines_from_steps(steps): results = [] decode = googlemaps.convert.decode_polyline for step in steps: pl = step['polyline'] locs = decode(pl['points']) locs = [[loc['lat'], loc['lng']] for loc in locs] results.extend(locs) return results locs = get_polylines_from_steps(steps) locs[:10] # [[36.05424, -112.14007000000001], # [36.05409, -112.14123000000001], # [36.05409, -112.14123000000001], # [36.054140000000004, -112.14124000000001], # [36.05418, -112.14126], # [36.05422, -112.14128000000001], # [36.05427, -112.14131], # [36.05431, -112.14135], # [36.05436, -112.14138000000001], # [36.05442, -112.14145]] m = folium.Map(location=[37.5, -111], zoom_start=7.0) m.line(locations=locs) m.simple_marker(locs[0], popup='Grand Canyon, AZ, USA') m.simple_marker(locs[-1], popup='Arches, UT, USA') inline_map(m)

まとめ
folium から Leaflet の以下の機能を利用する方法を記載した。
- シンプルマーカーの表示とクラスタ表示
- サークルの表示
- ポリラインの表示と Google Maps Direction API の利用

Pythonによるデータ分析入門 ―NumPy、pandasを使ったデータ処理
- 作者: Wes McKinney,小林儀匡,鈴木宏尚,瀬戸山雅人,滝口開資,野上大介
- 出版社/メーカー: オライリージャパン
- 発売日: 2013/12/26
- メディア: 大型本
- この商品を含むブログ (12件) を見る
10 Minutes to DataFrames.jl
この記事は Julia Advent Calendar 2015 23 日目の記事です。
Julia で DataFrame を扱うパッケージ DataFrames.jl の使い方をまとめたい。
下の pandas ドキュメントにあるような処理が DataFrames.jl でどう書けるのかを整理する。
versioninfo() # Julia Version 0.4.2 # Commit bb73f34 (2015-12-06 21:47 UTC)
インストール
Pkg.add("DataFrames") Pkg.installed("DataFrames") # v"0.6.10" using DataFrames
データの作成
DataFrames.jl では 1 次元データ構造である DataArray ( DataArrays.jl ) と 2 次元データ構造である DataFrame を扱う。それぞれ、R や Python ( pandas ) では以下のようなクラスに対応する。
Julia (DataFrames.jl) |
R | Python (pandas) |
|---|---|---|
DataArrays.DataArray |
atomic ( vector ) |
Series |
DataFrames.DataFrame |
data.frame |
DataFrame |
DataArrayの作成
DataArray は直接作成せず、@data マクロを利用して作るのがよい。@data マクロを使うとでは欠損値 ( NA ) をよしなに処理して DataArray 化してくれる。
s = @data([1, NA, 3]) # 3-element DataArrays.DataArray{Int64,1}: # 1 # NA # 3 # データの実体 s.data # 3-element Array{Int64,1}: # 1 # 1 # 3 # NA に対応するマスク s.na # 3-element BitArray{1}: # false # true # false # NG! [1, NA, 3] # LoadError: MethodError: `convert` has no method matching convert(::Type{Int64}, ::DataArrays.NAtype)
DataFrame の作成
作成したいデータの "列名 = Array" のペアを渡す。
df = DataFrame(A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], B = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1], C = ["A", "B", "C", "A", "B", "C", "A", "B", "C", "A"]) # 10x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|----|-----| # | 1 | 1 | 10 | "A" | # | 2 | 2 | 9 | "B" | # | 3 | 3 | 8 | "C" | # | 4 | 4 | 7 | "A" | # | 5 | 5 | 6 | "B" | # | 6 | 6 | 5 | "C" | # | 7 | 7 | 4 | "A" | # | 8 | 8 | 3 | "B" | # | 9 | 9 | 2 | "C" | # | 10 | 10 | 1 | "A" |
DataFrame の確認
各列の型は以下のようにして確認できる。colwise は関数を列ごとに適用する generic function。
typeof(df) # DataFrames.DataFrame colwise(typeof, df) # 3-element Array{Any,1}: # [DataArrays.DataArray{Int64,1}] # [DataArrays.DataArray{Int64,1}] # [DataArrays.DataArray{ASCIIString,1}] eltype(df) # Any colwise(eltype, df) # 3-element Array{Any,1}: # [Int64] # [Int64] # [ASCIIString]
列名の表示は names。行名や index にあたるものはない (行番号のみ)。
names(df) # 3-element Array{Symbol,1}: # :A # :B # :C
先頭 / 末尾のレコードを確認したい場合は head もしくは tail。既定では 6 レコード表示。
head(df) # 6x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|---|----|-----| # | 1 | 1 | 10 | "A" | # | 2 | 2 | 9 | "B" | # | 3 | 3 | 8 | "C" | # | 4 | 4 | 7 | "A" | # | 5 | 5 | 6 | "B" | # | 6 | 6 | 5 | "C" | tail(df, 3) # 3x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|---|-----| # | 1 | 8 | 3 | "B" | # | 2 | 9 | 2 | "C" | # | 3 | 10 | 1 | "A" |
要約統計量の表示は describe。これは表示のためだけの関数のようで、返り値は Void になる。
describe(df) # A # Min 1.0 # 1st Qu. 3.25 # Median 5.5 # Mean 5.5 # 3rd Qu. 7.75 # Max 10.0 # NAs 0 # NA% 0.0% # # B # Min 1.0 # 1st Qu. 3.25 # ... ... typeof(describe(df)) # Void
入出力
DataFrames.jl では CSV のみ。
writetable("data.csv", df) df = readtable("data.csv")
データの選択
行や列を選択する操作を記載する。
補足 DataFrame の出力の表示が一部 ドット (...) で省略されているが、これは自分が手動でやった。既定では全レコードが表示されるようだ。
位置、ラベルによる選択
R や pandas と同じく、引数をスカラーで渡すと返り値の次元が減って DataArray になる。
列名を指定する場合、引数は文字列ではなく Symbol として渡す必要があるようだ。Int を渡した場合は列番号での選択になる。
df[:A] # 10-element DataArrays.DataArray{Int64,1}: # 1 # 2 # ... # 9 # 10 # NG! df["A"] # LoadError: MethodError: `getindex` has no method matching getindex(::DataFrames.DataFrame, ::ASCIIString) df[Symbol("A")] # 略 df[1] # 略
対象を Array や UnitRange で指定すると 返り値は DataFrame となる。
df[[:A]] # 10x1 DataFrames.DataFrame # | Row | A | # |-----|----| # | 1 | 1 | # | 2 | 2 | # ... .. # | 9 | 9 | # | 10 | 10 | df[[1]] # 略 df[2:3] # 10x2 DataFrames.DataFrame # | Row | B | C | # |-----|----|-----| # | 1 | 10 | "A" | # | 2 | 9 | "B" | # ... .. ... # | 9 | 2 | "C" | # | 10 | 1 | "A" | df[[:B, :C]] # 略
行 / 列それぞれで指定したい場合は順番に引数として渡す。行番号のみで選択したい場合、第二引数に : を渡す。
df[5:7, :] # 3x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|---|---|-----| # | 1 | 5 | 6 | "B" | # | 2 | 6 | 5 | "C" | # | 3 | 7 | 4 | "A" | df[3:4, [:A, :B]] # 2x2 DataFrames.DataFrame # | Row | A | B | # |-----|---|---| # | 1 | 3 | 8 | # | 2 | 4 | 7 | df[2, :A] # 2
条件式による選択
julia の通常の演算子は element-wise ではない。element-wise に操作したい場合はドットで始まる演算子を使う。この仕様は明示的で良いと思う。
df[:A] == 0 # false df[:A] .== 0 # 10-element DataArrays.DataArray{Bool,1}: # false # false # ..... # false # false
上で作成した Array を使えば 対応する行のみが選択できる。
df[df[:A] .> 5, :] # 5x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|---|-----| # | 1 | 6 | 5 | "C" | # | 2 | 7 | 4 | "A" | # | 3 | 8 | 3 | "B" | # | 4 | 9 | 2 | "C" | # | 5 | 10 | 1 | "A" |
対応する element-wise 演算子がない場合は 内包表記を使って Bool の Array を作ればよい。
[in(x, ("A", "B")) for x in df[:C]] # 10-element Array{Bool,1}: # true # true # ..... # false # true df[[in(x, ("A", "B")) for x in df[:C]], :] # 7x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|----|-----| # | 1 | 1 | 10 | "A" | # | 2 | 2 | 9 | "B" | # ... .. .. ...| # | 6 | 8 | 3 | "B" | # | 7 | 10 | 1 | "A" |
代入
データ選択した箇所に値を代入できる。
df[[1, 4], :A] = NA df # 10x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|----|-----| # | 1 | NA | 10 | "A" | # | 2 | 2 | 9 | "B" | # | 3 | 3 | 8 | "C" | # | 4 | NA | 7 | "A" | # | 5 | 5 | 6 | "B" | # | 6 | 6 | 5 | "C" | # | 7 | 7 | 4 | "A" | # | 8 | 8 | 3 | "B" | # | 9 | 9 | 2 | "C" | # | 10 | 10 | 1 | "A" |
ソート
generic function を利用してソートできる。ソート対象の列や 順序などが引数で指定できる。関数名が ! で終わるものは破壊的な操作を行うもの。
sort(df, cols = :B) # 10x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|----|-----| # | 1 | 10 | 1 | "A" | # | 2 | 9 | 2 | "C" | # | 3 | 8 | 3 | "B" | # | 4 | 7 | 4 | "A" | # | 5 | 6 | 5 | "C" | # | 6 | 5 | 6 | "B" | # | 7 | NA | 7 | "A" | # | 8 | 3 | 8 | "C" | # | 9 | 2 | 9 | "B" | # | 10 | NA | 10 | "A" |
欠損値
欠損値 NA は DataArrays.jl にて定義されており、Built-in にある非数 NaN とは異なる。
typeof(NA) # DataArrays.NAtype NA == NA # NA NA + 1 # NA NA | true # true is(NA, NA) # true typeof(NaN) # Float64
Array の各要素が NA かどうか調べるには isna を使う。
isna(df[:A]) # 10-element BitArray{1}: # true # false # false # true # ..... # false # false df[isna(df[:A]), :] # 2x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|----|-----| # | 1 | NA | 10 | "A" | # | 2 | NA | 7 | "A" | df[~isna(df[:A]), :] # 8x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|---|-----| # | 1 | 2 | 9 | "B" | # | 2 | 3 | 8 | "C" | # | 3 | 5 | 6 | "B" | # | 4 | 6 | 5 | "C" | # | 5 | 7 | 4 | "A" | # | 6 | 8 | 3 | "B" | # | 7 | 9 | 2 | "C" | # | 8 | 10 | 1 | "A" |
ある列について NA を除きたければ dropna。NA を含む列を集約する場合に有用。
dropna(df[:A]) # 8-element Array{Int64,1}: # 2 # 3 # 5 # .. # 9 # 10 mean(df[:A]) # NA mean(dropna(df[:A])) # 6.25
欠損値をパディングしたい場合は データ選択して代入。ただし DataFrame に異なる型の列が含まれている場合は (実際には代入が発生しなくても) エラーになるため、列名も明示したほうがよい。
df[isna(df[:A]), :] = 0 # LoadError: MethodError: `convert` has no method matching convert(::Type{ASCIIString}, ::Int64) df[isna(df[:A]), :A] = 0 df # 10x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|----|----|-----| # | 1 | 0 | 10 | "A" | # | 2 | 2 | 9 | "B" | # | 3 | 3 | 8 | "C" | # | 4 | 0 | 7 | "A" | # ... .. .. ... # | 9 | 9 | 2 | "C" | # | 10 | 10 | 1 | "A" |
演算、集計
演算
DataArray 同士の演算は element-wise な演算になる。
df[:A] - df[:B] # 10-element DataArrays.DataArray{Int64,1}: # -10 # -7 # ... # 7 # 9
集計、集約
ある一つの列を集約したい場合は そのまま集約関数に渡せばよい。
mean(df[:B])
# 5.5
複数の列を集約したい場合は aggregate もしくは colwise。aggregate の結果は DataFrame に、colwise は Array{Any,1} になる。
aggregate(df[[:A, :B]], sum) # 1x2 DataFrames.DataFrame # | Row | A_sum | B_sum | # |-----|-------|-------| # | 1 | 50 | 55 | colwise(sum, df[[:A, :B]]) # 2-element Array{Any,1}: # [50] # [55]
aggregate では複数列 / 複数の集約関数で集計を行うこともできる。
aggregate(df, :C, mean) # 3x3 DataFrames.DataFrame # | Row | C | A_mean | B_mean | # |-----|-----|--------|--------| # | 1 | "A" | 4.25 | 5.5 | # | 2 | "B" | 5.0 | 6.0 | # | 3 | "C" | 6.0 | 5.0 | aggregate(df, :C, [mean, sum]) # 3x5 DataFrames.DataFrame # | Row | C | A_mean | A_sum | B_mean | B_sum | # |-----|-----|--------|-------|--------|-------| # | 1 | "A" | 4.25 | 17 | 5.5 | 22 | # | 2 | "B" | 5.0 | 15 | 6.0 | 18 | # | 3 | "C" | 6.0 | 18 | 5.0 | 15 |
グループ別に集約したい場合は by もしくは aggregate。
by(df, :C, x -> mean(x[:A])) # 3x2 DataFrames.DataFrame # | Row | C | x1 | # |-----|-----|------| # | 1 | "A" | 4.25 | # | 2 | "B" | 5.0 | # | 3 | "C" | 6.0 | aggregate(df, :C, mean) # 3x3 DataFrames.DataFrame # | Row | C | A_mean | B_mean | # |-----|-----|--------|--------| # | 1 | "A" | 4.25 | 1.25 | # | 2 | "B" | 5.0 | 6.0 | # | 3 | "C" | 6.0 | 5.0 |
関数適用
また colwise を使うと ラムダ式を各列に適用することもできる ( apply のような操作)。
colwise(x -> mean(x[1:5]) - mean(6:10), df[[:A, :B]]) # 2-element Array{Any,1}: # [-6.0] # [0.0]
連結、結合、変形
連結
以下 2 つの関数で行う。昔は rbind, cbind という関数があったようだが、すでに削除されている。
vcat:DataFrameを縦方向に連結。hcat:DataFrameを横方向に連結。
df1 = DataFrame(A = [1, 2, 3], B = [4, 5, 6]) df2 = DataFrame(A = [11, 12, 13], B = [14, 15, 16]) vcat(df1, df2) # 6x2 DataFrames.DataFrame # | Row | A | B | # |-----|----|----| # | 1 | 1 | 4 | # | 2 | 2 | 5 | # | 3 | 3 | 6 | # | 4 | 11 | 14 | # | 5 | 12 | 15 | # | 6 | 13 | 16 | df3 = DataFrame(A = [1, 2, 3], B = [4, 5, 6]) df4 = DataFrame(C = [11, 12, 13], D = [14, 15, 16]) hcat(df3, df4) # 3x4 DataFrames.DataFrame # | Row | A | B | C | D | # |-----|---|---|----|----| # | 1 | 1 | 4 | 11 | 14 | # | 2 | 2 | 5 | 12 | 15 | # | 3 | 3 | 6 | 13 | 16 |
結合
特定の列の値で結合するには join。結合方法は kind で指定できる。一通りの結合方法は揃っている。
left = DataFrame(A = [1, 2, 3], B = [11, 12, 13]) right= DataFrame(A = [2, 3, 4], C = [12, 13, 14]) join(left, right, on = :A) # 2x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|---|----|----| # | 1 | 2 | 12 | 12 | # | 2 | 3 | 13 | 13 | join(left, right, on = :A, kind = :outer) # 4x3 DataFrames.DataFrame # | Row | A | B | C | # |-----|---|----|----| # | 1 | 2 | 12 | 12 | # | 2 | 3 | 13 | 13 | # | 3 | 1 | 11 | NA | # | 4 | 4 | NA | 14 |
変形
いわゆる tidy なデータへの変換と逆変換。
stack,melt: 列持ち → 行持ちへの変換 (unpivot)。unstack: 行持ち → 列持ちへの変換 (pivot)。
df5 = DataFrame(Name = ["A", "B", "C", "D"], width = [1, 2, 3, 4], height = [10, 20, 30, 40]) stacked = stack(df5, [:width, :height]) # 8x3 DataFrames.DataFrame # | Row | variable | value | Name | # |-----|----------|-------|------| # | 1 | width | 1 | "A" | # | 2 | width | 2 | "B" | # | 3 | width | 3 | "C" | # | 4 | width | 4 | "D" | # | 5 | height | 10 | "A" | # | 6 | height | 20 | "B" | # | 7 | height | 30 | "C" | # | 8 | height | 40 | "D" | melt(df5, :Name) # 略 unstack(stacked, :Name, :variable, :value) # 4x3 DataFrames.DataFrame # | Row | variable | height | width | # |-----|----------|--------|-------| # | 1 | "A" | 10 | 1 | # | 2 | "B" | 20 | 2 | # | 3 | "C" | 30 | 3 | # | 4 | "D" | 40 | 4 |
データ型固有の処理
データ型に固有の操作を記載する。pandas ではデータ型固有の操作をまとめた .str, .dt などのアクセサがあるが、DataFrames.jl にはそれらに相当するものはなさそうだ。
標準の関数は一部 Array にも適用できるが、そうでない場合は 内包表記を使ってデータを操作する。
日時型
標準には Datetime と Period 二つの型がある。Python でいうと datetime と timedelta + 一部 relativedelta に相当する型だ。これらは DataArray や DataFrame に値として含めることができる。
DataFrames.jl としてはリサンプリングやタイムゾーンなどは機能として持っていない。
dates = @data([DateTime(2013, 01, i) for i in 1:4]) # 6-element DataArrays.DataArray{DateTime,1}: # 2013-01-01T00:00:00 # 2013-01-02T00:00:00 # 2013-01-03T00:00:00 # 2013-01-04T00:00:00 # DateTime から日付を取得 Dates.day(dates) # 4-element Array{Union{DataArrays.NAtype,Int64},1}: # 1 # 2 # 3 # 4 # DateTime を Period に変換 periods = [Dates.Year(d) for d in dates] # 4-element Array{Base.Dates.Year,1}: # 2013 years # 2013 years # 2013 years # 2013 years [DateTime(p) for p in periods] # 4-element Array{Any,1}: # 2013-01-01T00:00:00 # 2013-01-01T00:00:00 # 2013-01-01T00:00:00 # 2013-01-01T00:00:00
時系列については別のパッケージがあるため、こちらを使うのがよいのかもしれない。
文字列型
それぞれ 内包表記で処理する。
lowercase(df[:C]) # LoadError: MethodError: `lowercase` has no method matching lowercase(::DataArrays.DataArray{ASCIIString,1}) [lowercase(x) for x in df[:C]] # 10-element Array{Any,1}: # "a" # "b" # ... # "c" # "a"
カテゴリカル型
いわゆるカテゴリカル型はない。Array の利用メモリを削減するための PooledDataArray というクラスがある。
まとめ
DataFrames.jl でのデータ操作を整理した。
API や 使い勝手は pandas よりも R の data.frame に近い感じだ (ただし dplyr は存在しない )。Julia にはパイプ演算子があるため、pandas よりは dplyr のようなパッケージがあると流行りそうだ。