Rust で k-means クラスタリング
この記事は Rust Advent Calendar 2015 7 日目の記事です。
簡単な統計/機械学習のアルゴリズムを実装しつつ Rust を学びたい。こちらの続き。
環境:
- Rust(Nightly) rustc 1.6.0-nightly (d49e36552 2015-12-05)
- rust-csv 0.14.3 : CSV の読み込みに利用
- nalgebra 0.3.2 : 行列/ベクトルの処理に利用
- rand 0.3.12 : 乱数生成に利用
- gnuplot 0.0.19 : プロットに利用
k-means クラスタリングとは
非階層型クラスタリングの一種。下のアニメーションがわかりやすい。
Rust でプロット
これまでは 結果を数値で表示するだけだったが、味気ないのでプロットを出力したい。検索したところ gnuplot の Rust 用 wrapper があった。
extern crate gnuplot; use gnuplot::{Figure, Color}; fn main() { let mut fg = Figure::new(); fg.axes2d() .lines(&[1, 2, 3], &[4, 5, 6], &[Color("blue")]) .lines(&[1, 2, 3], &[7, 6, 5], &[Color("red")]); fg.set_terminal("png", "test.png"); fg.show(); }

描画するオブジェクト (上の例では .lines) は fg.axes2d() からチェインさせて呼び出すことが推奨されているようだ。 let ax = fg.axes2d() など変数に代入してしまうと fg の所有権が move したままとなり、 fg.show() で描画できない状態になってしまう。
が、それではデータを逐次描画していくことができないため、以下の例ではすこし変わった書き方をしている。
Rust で k-means
前回まで作ったものを Crate にして、必要なクラス、関数を再利用している。
extern crate csv; extern crate gnuplot; extern crate nalgebra; extern crate num; extern crate rand; extern crate brasswheels; use gnuplot::{Figure, Color}; use nalgebra::{DVec, DMat, RowSlice, Iterable}; use rand::sample; use std::collections::HashMap; use std::f64; use std::ops::Index; use brasswheels::io::read_csv_f64; // CSV から f64 型のみを読みこむ use brasswheels::pca::PCA; // 主成分分析 use brasswheels::mathfunc::euc_dist; // 2 つのベクトルのユークリッド距離を求める fn main() { // http://aima.cs.berkeley.edu/data/iris.csv let path = "./data/iris.csv"; let mut reader = csv::Reader::from_file(path).unwrap().has_headers(false); let dx = read_csv_f64(&mut reader); // k-means (クラスタ数, 最大のイテレーション数) let mut kmeans = KMeans::new(3, 300); kmeans.fit(&dx); println!("各クラスタの中心点"); for (_, cluster) in &kmeans.centroids { println!("{:?}", cluster.centroid.at); } let predicted = kmeans.predict(&dx); println!("クラスタリング結果\n{:?}", &predicted.at); // 2 次元に描画するため主成分分析を行う let mut pca = PCA::new(4, true); pca.fit(&dx); let transformed = pca.transform(&dx); // プロット // http://siegelord.github.io/RustGnuplot/doc/gnuplot/struct.Axes2D.html let mut fg = Figure::new(); let colors = ["blue", "red", "green"]; // fg.axes2d() によって fg が move するため、 // 同一ブロック中で呼び出すと fg.show() が使えなくなる (0..kmeans.nclusters).fold(fg.axes2d(), |ax, c| { let mut xvals: Vec<f64> = vec![]; let mut yvals: Vec<f64> = vec![]; for (rownum, &predc) in predicted.iter().enumerate() { if predc == c { xvals.push(*transformed.index((rownum, 0))); yvals.push(*transformed.index((rownum, 1))); } } return ax.points(&xvals, &yvals, &[Color(colors[c])]); }); fg.set_terminal("png", "kmeans.png"); fg.show(); } pub struct KMeans { pub nclusters: usize, // クラスタ数 max_iter: usize, // イテレーション回数 pub centroids: HashMap<usize, Cluster>, } impl KMeans { pub fn new(nclusters: usize, max_iter: usize) -> KMeans { KMeans { nclusters: nclusters, max_iter: max_iter, centroids: HashMap::new(), } } pub fn fit(&mut self, data: &DMat<f64>) { let mut rng = rand::thread_rng(); // データからクラスタの初期値をサンプリング (非復元抽出) let inits: Vec<usize> = sample(&mut rng, 0..data.nrows(), self.nclusters); for (i, rownum) in inits.into_iter().enumerate() { let mut c = Cluster::new(data.ncols()); let row = data.row_slice(rownum, 0, data.ncols()); c.add_element(row); self.centroids.insert(i, c); } let mut cindexer = self.predict(data); // 最大 max_iter 回繰り返し for _ in 0..self.max_iter { // 中心点の更新 self.update_centroids(&data, &cindexer); // 各レコードを クラスタの中心点にもっとも近いものに分類 let cindexer_new = self.predict(data); // Eq での比較結果は element-wise ではなく bool になる if cindexer_new == cindexer { // 変化がなくなったら終了 break; } else { cindexer = cindexer_new; } } } /// 各レコードが所属するクラスタのベクトルを返す pub fn predict(&self, data: &DMat<f64>) -> DVec<usize> { return DVec::from_fn(data.nrows(), |x| self.get_nearest(&data.row_slice(x, 0, data.ncols()))); } /// レコードにもっとも近い中心点をもつクラスタのラベルを返す fn get_nearest(&self, values: &DVec<f64>) -> usize { let mut tmp_i = 0; let mut current_dist = f64::MAX; for (cnum, cluster) in &self.centroids { let d = euc_dist(values, &cluster.centroid); if d < current_dist { current_dist = d; tmp_i = *cnum; } } return tmp_i; } /// クラスタの中心点を更新する fn update_centroids(&mut self, data: &DMat<f64>, cindexer: &DVec<usize>) { self.centroids.clear(); for i in 0..self.nclusters { let c = Cluster::new(data.ncols()); self.centroids.insert(i, c); } for (rownum, cnum) in cindexer.iter().enumerate() { let row = data.row_slice(rownum, 0, data.ncols()); let mut c = self.centroids.remove(&cnum).unwrap(); c.add_element(row); self.centroids.insert(*cnum, c); } for cnum in 0..self.nclusters { let mut c = self.centroids.remove(&cnum).unwrap(); c.finalize(); self.centroids.insert(cnum, c); } } } pub struct Cluster { pub centroid: DVec<f64>, n: f64 } impl Cluster { fn new(ncols: usize) -> Cluster { Cluster { centroid: DVec::from_elem(ncols, 0.), n: 0. } } /// 中心点を更新 (レコードを合計に追加する) fn add_element(&mut self, values: DVec<f64>) { self.centroid = self.centroid.clone() + values; self.n = self.n + 1.; } /// 中心点を更新 (レコード数で割り、中心点を求める) fn finalize(&mut self) { if self.n != 0. { self.centroid = self.centroid.clone() / self.n; self.n = 0.; } } }
結果の出力。
各クラスタの中心点 # [5.005999999999999, 3.4180000000000006, 1.464, 0.2439999999999999] # [5.88360655737705, 2.740983606557377, 4.388524590163935, 1.4344262295081966] # [6.853846153846153, 3.0769230769230766, 5.715384615384615, 2.053846153846153] クラスタリング結果 # [2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, # 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, # 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, # 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, # 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, # 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1]
クラスタごとに色分けしてプロットすると以下のようになる。うまくクラスタリングできているようだ。
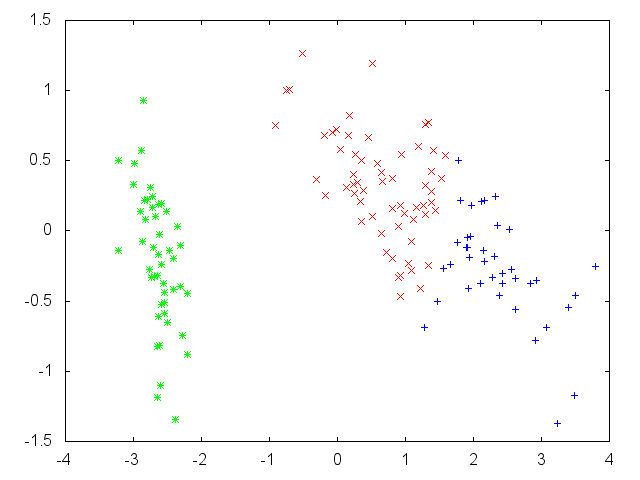
R の結果。初期値の選ばれ方次第で中心点の順序が変わる / 差異がより大きくなる場合もある。
biris = read.csv("iris.csv", header=FALSE) kmeans(biris[-5], 3)$centers # V1 V2 V3 V4 # 1 5.006000 3.418000 1.464000 0.244000 # 2 5.901613 2.748387 4.393548 1.433871 # 3 6.850000 3.073684 5.742105 2.071053