Python networkx でマルコフ確率場 / 確率伝搬法を実装する
ここ 1ヶ月にわたって 聖書 DeepLearning 0.1 Documentation を読み進め、ようやく 制約付きボルツマンマシン の手前まできた。
制約付きボルツマンマシン (RBM) の解説 には RBM = マルコフ確率場 ( Markov Random Field / MRF ) の一種だよっ、と しれっと書いてあるのだが マルコフ確率場とはいったい何なのかは説明がない。マルコフ確率場 <マルコフ・ランダム・フィールド> は用語もカッコイイし結構おもしろいので、 Python でサンプルを書いてみる。
補足 Python では PyStruct というパッケージがマルコフ確率場 / 条件付き確率場 ( Conditional Random Field ) を実装しているため、実用したい方はこちらを。このパッケージ、ノーマークだったがよさげだなあ。
マルコフ確率場とは
グラフィカルモデルの一種。グラフィカルモデルとは、確率変数間の関係をグラフとしてあらわしたモデル。以下の資料が非常にわかりやすい。
さらに詳しくはPRML。

Pattern Recognition and Machine Learning (Information Science and Statistics)
- 作者: Christopher Bishop
- 出版社/メーカー: Springer
- 発売日: 2010/02/15
- メディア: ハードカバー
- 購入: 5人 クリック: 67回
- この商品を含むブログ (29件) を見る
マルコフ確率場のサンプル
今回はマルコフ確率場を使って画像のノイズ除去をしてみる。そのため、以下のような構造をもつマルコフ確率場をグラフとしてモデル化する。
- 観測値はノイズを含む入力画像、潜在変数はノイズを除去した画像に対応。
- 観測値、潜在変数ともとりうる値は {0, 1} いずれか ( 2値画像 )。
- 観測値、潜在変数 それぞれ 1 画素 (ピクセル) に対し 1 ノードが対応。つまりノード総数は 画像の画素数 x 2。
- 観測値ノードは、同じ座標の 潜在変数ノードと 1:1 で接続。
- 潜在変数ノードは、自身の 上下左右にある 4 ノードと接続。ただし端点は接続できるノードにだけ接続。
上のモデルで仮定されるのは以下になる (というか以下の仮定のもとに上のモデルが作られている)。
- 潜在変数は、それぞれ隣接するノードからのみ 直接的な影響を受ける
- 誤差 (ノイズ) は画素ごとに独立である
イメージ図を描くと以下のようになる。グレーのノードは観測値であり、画像が入力された時点で値が確定する。この状態から、潜在変数のありえそうな状態 (ノイズを除去した画像) を推定する。

補足 上の構造は一例であり、必ずこうしなければならない! というものではない。ここがグラフィカルモデルのよい点であり、最初はとまどう点でもあると思う。何か別の仮定が存在する場合はそれにあわせてモデル (グラフ構造) を変える。
補足 また、上記のマルコフ確率場は制約付きボルツマンマシンでの考え方とは異なる。あくまでノイズ除去の場合のサンプル。
マルコフ確率場の実装に必要なグラフ構造の作成には networkx パッケージ (後述) を利用する。
確率伝搬法
マルコフ確率場の潜在変数の値を推定する方法。詳細は 上記の "いまさら聞けないグラフィカルモデリング入門" の "積和アルゴリズム" の箇所を。いや手抜きではなくて自分が変なこと書くよりわかりやすいと思うので、、、。
ここでは今回実装した 確率伝搬法の考え方を図示する。確率伝搬法についても、必ずしも今回実装したような動きをするわけではない。例えば、以下はモデルによって変わりうる。
- 各ノードをどの順番で走査するか: 以下の例では 横 -> 縦方向に全ノードを走査
- 周辺分布の計算 & 伝搬をどの範囲まで行うか: 以下の例では、対象ノードに隣接するノード + 隣接ノードに隣接するノード = 2 つ先まで
- 周辺分布の計算時に重み付けするかどうか: 以下の例では重み付けしない
- 伝搬が収束したとみなす条件
アルゴリズム
|
|
|
|
|
|
|
|
|
|
|
|
補足 後述のサンプルプログラムでは上の動きを 1 ステップずつ処理しているわけではない。例えば各潜在変数の周辺分布は収束するまで計算する必要がない (確率伝搬に必要な部分のみ計算する)。また、処理順序も効率的になるように変えている (最終的に同じ処理が行われるようにしている)。
補足 Propagation の訳語は Wikipedia の表記を一般的なものとみなしてあわせた。
参考 【機械学習】"Propagation"の訳は「伝播」or「伝搬」? - 歩いたら休め
次から実装のはなし。
networkx の簡単な使い方
まず、サンプル中で利用する networkx パッケージの概要を記載する。networkx は各種グラフ (有向、無向、多重) の作成や経路探索などができるパッケージ。
インストール
pip で OK。
pip install networkx
グラフの作成
今回の例では以下の方法は使わないのだが、基本的なグラフの作り方を。
networkx.Graph: 空の無向グラフ インスタンスを作成する。networkx.Graph.add_node: グラフにノードを追加する。引数はノードのキー。ここでは 2次元のグラフを作る想定のため、キーとして長さ 2 のtupleを渡しているが、ハッシュ化可能なもの (文字列とか) は何でもキーにできる。networkx.Graph.add_edge: グラフのノード間にエッジを追加する。引数は接続される ノードのキー 2 コ。今回は 無向グラフなので順序は関係ない。
import networkx as nx # グラフ作成 g = nx.Graph() # ノード (0, 0) を追加 g.add_node((0, 0)) # ノード (0, 1) を追加 g.add_node((0, 1)) # ノード (0, 0) と (0,1) の間にエッジを追加 g.add_edge((0,0), (0, 1))
グラフの描画 (プロット)
描画方法に応じて いくつかの関数が用意されている。詳細は以下ドキュメントを。
import matplotlib.pyplot as plt nx.draw_networkx(g, node_color='w') plt.gca().xaxis.set_visible(False) plt.gca().yaxis.set_visible(False) plt.show()
先ほど作成したグラフ ( 2 ノード、1 エッジ ) が描画される。

格子グラフの作成
今回 作成したい 2次元の格子グラフは networkx.grid_2d_graph で簡単に作成できる。マルコフ確率場の作成にはこちらを利用する。
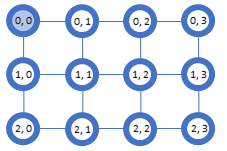
3 行 3 列の格子グラフを作成し描画してみる。グラフを描画する際に、 pos キーワードを使うと 各ノードの描画位置を指定できる。
nw = nx.grid_2d_graph(3, 3) # 各ノードの描画位置を指定する辞書 { ノードのキー : (x座標, y座標) } pos = {n: (n[0], -n[1]) for n in nw.nodes()} pos # {(0, 1): (0, -1), (1, 2): (1, -2), (0, 0): (0, 0), # (2, 1): (2, -1), (0, 2): (0, -2), (2, 0): (2, 0), # (2, 2): (2, -2), (1, 0): (1, 0), (1, 1): (1, -1)} nx.draw_networkx(nw, pos=pos, node_color='w') plt.gca().xaxis.set_visible(False) plt.gca().yaxis.set_visible(False) plt.show()

マルコフ確率場のサンプルプログラム
MNISTデータに 5% のノイズを加え、マルコフ確率場によってノイズ除去を行うサンプルプログラムを作成した。元画像、ノイズ付与した画像、マルコフ確率場でのノイズ除去結果 (推測値) をプロットすると以下のような感じになる。そこそこうまくノイズ除去できていることがわかる。
- 単一画素のノイズはほぼ消えている
- 元画像に存在する細い線も (ノイズとみなされて) 消えてしまうことがある。

プログラムは gist においた。考え方は上で記載したアルゴリズムにもとづくが、処理の順序はプログラムがより単純になるよう変えている。
12/28追記 一部コメント / 用語の不一致を修正。