R で 状態空間モデル: {dlm} の最尤推定を可視化する

{dlm} において、状態空間モデルが最尤推定される過程がみたい。以下内容の補足的なエントリ。

sinhrks.hatenablog.com

「状態空間時系列分析入門」では 引き続き 第8章 に相当。

状態空間時系列分析入門

データの準備

データは著者のサポートサイト、An Introduction to State Space Time Series Analysis から入手できる。

library(dlm)
# install_github('sinhrks/ggfortify')
library(ggfortify)

ukdrivers <- read.table('UKdriversKSI.txt', skip = 1)
ukdrivers <- ts(ukdrivers[[1]], start = c(1969, 1), frequency = 12)
ukdrivers <- log(ukdrivers)

y <- ukdrivers

モデルの作成と状態推定値のプロット

サンプルとして、第3章3節 確率的レベルと確定的傾きをもつローカル線形トレンドモデル を作成する。

parm <- log(c(var(y), 0.001))
buildFun <- function(parm){
  dlmModPoly(order = 2, dV = exp(parm[1]), dW = c(exp(parm[2]), 0))
}
dlmFit <- dlmMLE(y, parm = parm, build = buildFun)

# カルマンフィルタ
dlmFiltered <- dlmFilter(y, buildFun(dlmFit$par))

# 平滑化
dlmSmoothed <- dlmSmooth(y, buildFun(dlmFit$par))

第8章ではモデルの推定値として 3 つの値が出てくるため、その差異がわかるようにプロットする。用語は状態空間時系列分析入門のものを利用。

p <- autoplot(y)
p <- autoplot(dlmFiltered$a[, 1], colour = 'red', linetype = 'dashed', p = p)
p <- autoplot(dlmFiltered$m[, 1], colour = 'red', p = p)
p <- autoplot(dlmSmoothed, colour = 'blue', p = p)
p + ylim(c(6.8, 8))

• 黒実線 ( y ): 観測時系列
• 赤破線 ( dlmFiltered$a ): カルマンフィルタの1期先予測 (予測ステップでの予測値)
• 赤実線 ( dlmFiltered$m ): カルマンフィルタのフィルタ化状態 (更新ステップでの予測値)
• 青実線 ( dlmSmoothed ): 平滑化状態

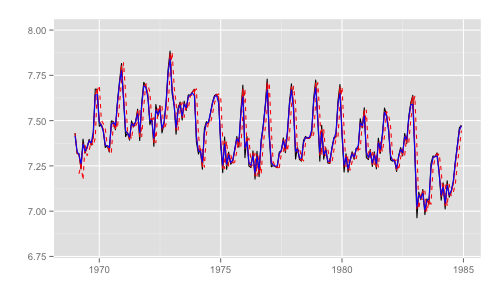
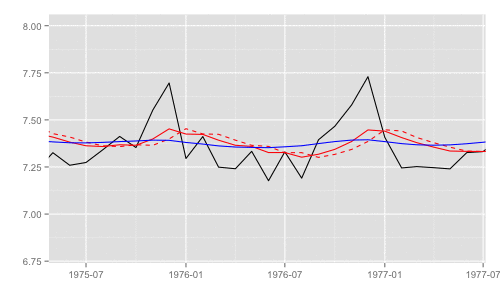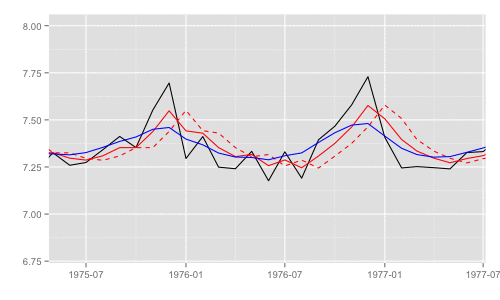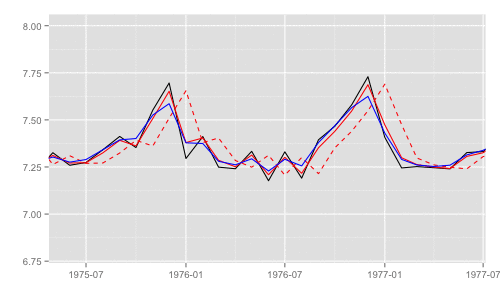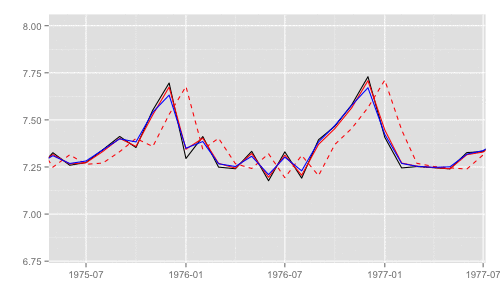
一部期間を拡大するとそれぞれの差異がわかる。これらのうち、最尤推定時の尤度計算式中で直接 利用されるのは "1期先予測" 時の予測誤差 (赤破線) とその標準偏差。

p + xlim(as.Date('1975', '%Y'), as.Date('1977', '%Y')) + ylim(c(6.8, 8))

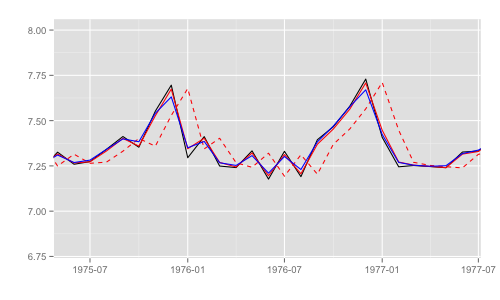
補足 上のモデルでは FF = [1, 0] のため、観測値の推定値 == 状態推定値。

dlmFiltered$mod$FF
#      [,1] [,2]
# [1,]    1    0

all((dlmFiltered$a %*% t(dlmFiltered$mod$FF)) == dlmFiltered$a[, 1])
# [1] TRUE

補足 カルマンフィルタの動きについては以前こんなエントリを書いた。2つ目のエントリにカルマンフィルタの予測 / フィルタ化状態がどういった感じで動いているか記載がある (平滑化は記載ない)。

• KalmanFilter の動きを可視化する 一次元版 - StatsFragments
• KalmanFilter の動きを可視化する 二次元版 - StatsFragments

予測誤差と予測誤差分散

最尤推定の尤度計算式は先のエントリに記載。計算に必要な (1期先) 予測誤差と予測誤差標準偏差は dlm:::residuals.dlmFiltered で求めることができる。

# 既定では標準化されるため、 type = 'raw' を指定して実値をとる
resid <- residuals(dlmFiltered, type = 'raw')

# 予測誤差
resid$res[1:12]
#  [1]  7.430707083 -3.827523556  0.111504168 -0.021616238  0.225665269 -0.044983932
#  [7]  0.045295381  0.061233329 -0.021088564  0.049603994  0.270853650  0.007138991

# 予測誤差標準偏差
resid$sd[1:12]
#  [1] 4472.1359566 2236.0679824    0.1922632    0.1596384    0.1484746    0.1429560
#  [7]    0.1396797    0.1375109    0.1359691    0.1348166    0.1339224    0.1332084

ふつうに計算して求めるなら、dlm::dlmFiltered インスタンスの各プロパティを利用して、

# 予測誤差
(y - (matrix(as.numeric(dlmFiltered$a), 192, 2) %*% t(dlmFiltered$mod$FF)))[1:12]
#  [1]  7.430707083 -3.827523556  0.111504168 -0.021616238  0.225665269 -0.044983932
#  [7]  0.045295381  0.061233329 -0.021088564  0.049603994  0.270853650  0.007138991

# もしくは
(y - dlmFiltered$f)[1:12]
#  [1]  7.430707083 -3.827523556  0.111504168 -0.021616238  0.225665269 -0.044983932
#  [7]  0.045295381  0.061233329 -0.021088564  0.049603994  0.270853650  0.007138991

# 予測誤差標準偏差
f <-  function(i) {
  FF <- dlmFiltered$mod$FF
  V <- dlmFiltered$mod$V
  diag(crossprod(dlmFiltered$D.R[i, ] * t(FF %*% dlmFiltered$U.R[[i]])) + V)
}
drop(t(sqrt(sapply(seq(along = dlmFiltered$U.R), f))))[1:12]
#  [1] 4472.1359566 2236.0679824    0.1922632    0.1596384    0.1484746    0.1429560
#  [7]    0.1396797    0.1375109    0.1359691    0.1348166    0.1339224    0.1332084

最尤推定の可視化

最尤推定時のパラメータの変化を記録するため、dlm::dlmMLE を書き換えた関数を定義する。LL_ckbookcompat はテキスト記載の対数尤度 (に近いもの) を計算するための関数 ( 詳細はこちら )。

# optim 1 ステップごとに作成されたモデルを保存
models <<- list()

dlmMLE_wrapper <- function (y, parm, build, method = "L-BFGS-B",
                            ..., debug = FALSE) {
  logLik <- function(parm, ...) {
    mod <- build(parm, ...)
    # グローバル変数に追加
    models[[length(models) + 1]] <<- mod
    return(dlmLL(y = y, mod = mod, debug = debug))
  }
  return(optim(parm, logLik, method = method, ...))
}

# 推定するパラメータ数が 2 のため、総和をとる範囲を変更
LL_ckbookcompat <- function(y, mod) {
  n <- length(y)
  filtered <- dlmFilter(y, mod)
  resid <- residuals_dlmcompat(filtered) 
  F <- (as.numeric(resid$sd)^2)[3:n]
  v <- as.numeric(resid$res)[3:n]
  return(-0.5 * (n * log(2 * pi) + sum(log(F) + (v^2/F))))
}

続けて、アニメーション用の処理を定義して実行。

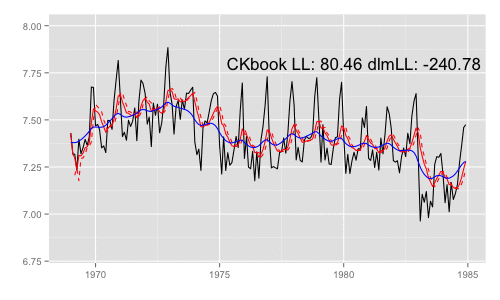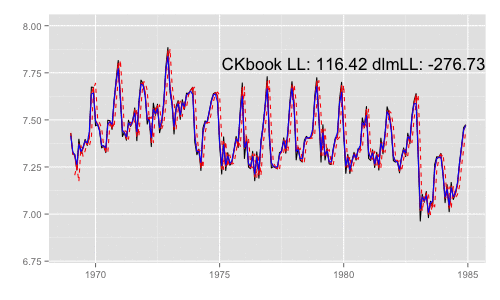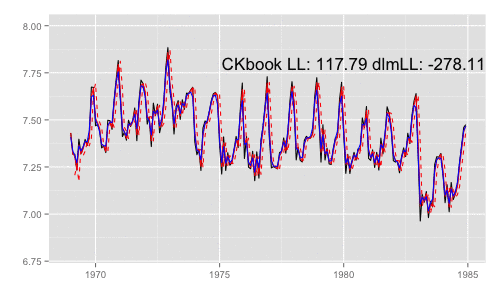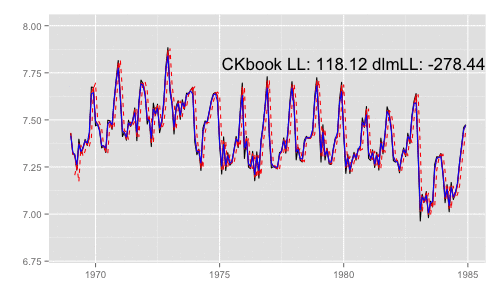
library(animation)

models <<- list()
dlmMLE_wrapper(y, parm = parm, build = buildFun)

saveGIF({
  for (mod in models[1:65]) {
    filtered <- dlmFilter(y, mod)
    p <- autoplot(filtered, fitted.colour = 'red', fitted.linetype = 'dashed')
    p <- autoplot(dlmSmooth(y, mod), colour = 'blue', p = p)
    label <- paste('CKbook LL:', round(LL_ckbookcompat(y, mod), 2), 'dlmLL:', round(dlmLL(y, mod), 2))
    p <- p + annotate('text', label = label, x = as.Date('1980', '%Y'), y = 7.8, size = 6)
    print(p)
    Sys.sleep(0.01)
  }
}, interval = 0.3, movie.name =  "dlm.gif",
ani.width = 500, ani.height = 300)

最尤推定時に各状態推定値がどのように変化していくかをみる。左側 "CKbookLL" はテキスト記載の対数尤度計算式 LL_ckbookcompat の値。右側 "dlmLL" は dlm::dlmLL の値 ( optim で最適化される値 )。

テキストに記載された数値より、収束時には左側の値が 0.6247935 x 観測時系列の長さ (192) = 119.9604 程度になるはずだ。

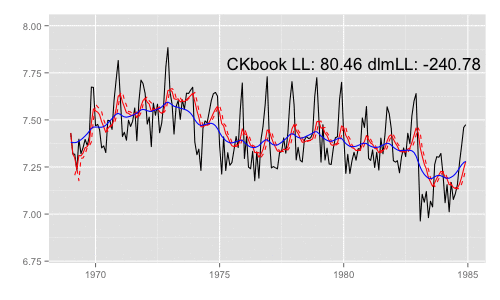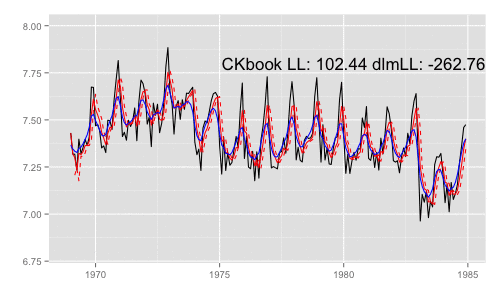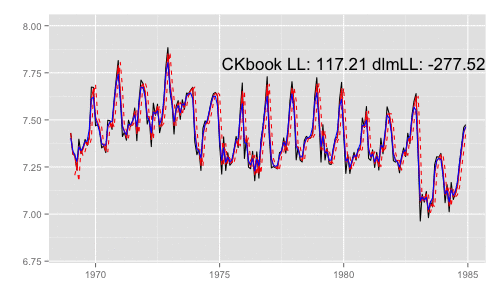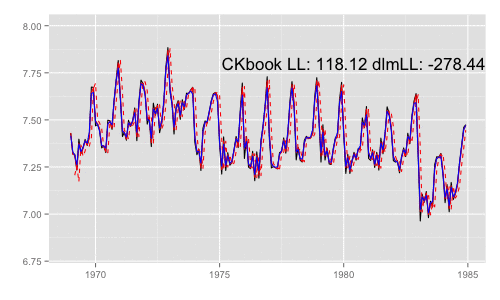
補足 {dlm} は既定では optim の際に method = 'L-BFGS-B' を利用する。可視化目的であれば Nelder-Mead 法なんかを使ったほうが 素人目には "最適化らしい" 動きになる気がする。

models <<- list()
dlmMLE_wrapper(y, parm = parm, build = buildFun,  method = 'Nelder-Mead')
# 以降略