Theano で Deep Learning <6の準備>: ホップフィールドネットワーク
DeepLearning 0.1 Documentation の第六回は 制約付きボルツマンマシン (Restricted Boltzmann Machines / RBM) なのだが、文書/内容とも結構 ボリュームがあるので外堀から埋めていきたい。
そのため、今回は ボルツマンマシンの前身である ホップフィールドネットワークを Python で書いてみる。
目次
DeepLearning 0.1 より、
| 第一回 MNIST データをロジスティック回帰で判別する | 英 |
| 第二回 多層パーセプトロン | 英 |
| 第三回 畳み込みニューラルネットワーク | 英 |
| 第四回 Denoising オートエンコーダ | 英 |
| 第五回 多層 Denoising オートエンコーダ | 英 |
| 第六回の準備1 networkx でマルコフ確率場 / 確率伝搬法を実装する | - |
| 第六回の準備2 ホップフィールドネットワーク (今回) | - |
| 第六回 制約付きボルツマンマシン | 英 |
| Deep Belief Networks | 英 |
| Hybrid Monte-Carlo Sampling | 英 |
| Recurrent Neural Networks with Word Embeddings | 英 |
| LSTM Networks for Sentiment Analysis | 英 |
| Modeling and generating sequences of polyphonic music with the RNN-RBM | 英 |
ホップフィールド ネットワーク ( Hopfield Networks ) とは
ホップフィールドネットワーク ( 以降 HNN )は与えられた複数のデータを記憶し、入力をもとに記憶したデータを思い出すことができる。日本語で説明しているサイトもあるのだが、それぞれ書いてあることに微妙に差異があったりするので、 英語版 Wikipedia と MITのテキスト にもとづいて書く。
HNN は、大きく 以下2段階の動作をする。
- 学習 ( Training ): 与えられた学習データをネットワークの内部状態として記憶する
- 更新 ( Updating ): 新しい入力値を受け取り、学習したデータのうちどれに近いかを思い出して出力する
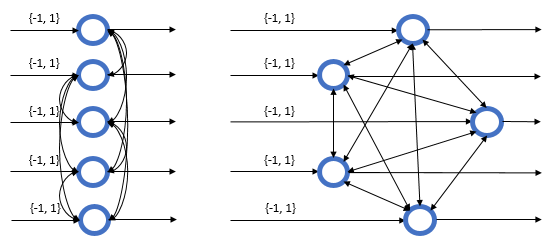
HNN のイメージ図を書くと以下のようになる。左右どちらの図も同じ構造をあらわしている。HNN は 循環ニューラルネットワーク ( Recurrent Neural Networks ) の一種で、ノードは 入力データの次元と同じ数だけ存在し、自分以外のすべてのノードと相互に接続するという循環する構造をもつ。このとき、ノード間の各接続重みは対称 (ノード i から j の接続重み = ノード j から i の接続重み ) となる。これは次元 (入力データの次元 x 入力データの次元) の重み行列 としてあらわせる。また 2 値の入力 / 出力については {0, 1} ではなく {-1, 1} と考えたほうがわかりやすいため、それにならう。
学習 ( Training )
学習データから内部状態 ( 重み行列 )を更新し、学習データをネットワークに記憶する処理。
今、 個の学習データをホップフィールドネットワークに記憶させたいとする。このとき、重み行列
の
成分
は、
番目の学習データの
成分
を使って 以下のように初期化される。これを ヘッブ則 ( ヘブ則 / Hebbian rule ) という。
つまり、重み行列を 番目の学習データ
であらわすと、
ただし、対角成分は となる。定義より
は対称行列になる。
データが {-1, 1} の 2値であることをふまえると、上では学習データの 成分に相関がある場合に 対応する重み行列の要素を増やす / 相関がなければ 減らすことでネットワークを初期化していることになる。
なぜこれで複数の状態を記憶できるのか?というのは ( HNN と若干定義が違うが) 以下の説明がわかりやすい。
更新 ( Updating )
未知データを入力値として受け取り、内部状態を元に各ユニットの状態を更新 & 出力を行う処理。 番目のユニット
の状態は以下の式で更新される。ユニットの状態が収束する (後述) まで更新を繰り返し、収束したときのユニットの状態が出力値になる。
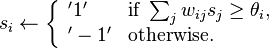
補足 はユニット活性化の閾値ベクトル。上式のとおり、閾値は符号が逆のバイアスを与えることと同じ (閾値 = -バイアス)。今回は閾値
として、全ユニットに共通の閾値を与える。
1/12追記 閾値とバイアスの関係について説明追加。閾値 / バイアスを混同した誤記を修正。
更新には以下 2通りの方法があり、今回は前者の方法を用いる。
- 同期 ( Synchronous ): 全ユニットをまとめて状態更新する
- 非同期 ( Asynchronous ): ランダムに選択した1ユニットの状態を更新する
このとき、重み行列と更新後の各ユニットの状態ベクトル は以下の関係にある。
はベクトルの各要素が 閾値
より大きいなら 1, それ以外なら -1 を割り当てる階段関数。この階段関数を各ユニットの活性化関数と考えることができる。
つまり HNN の更新処理とは、ユニットの状態 が変化しなくなるまで "重み行列をかけて階段関数適用" のループをまわすことと同じ。
ネットワーク エネルギー
HNN では、ある時点のユニットの状態 / 重み行列 / 閾値をもとに ネットワークのエネルギー を定義している。各ユニットの状態が更新されるたびにこのエネルギーは減っていき、ユニットの状態が収束するとエネルギーは一定になる。このときの各ユニットの状態が HNN からの出力値になる。が、必ずしも広域最適解が求められるとは限らない。
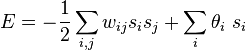
なぜ更新によってエネルギーが減少するのか?という点は以下のサイトの説明がわかりやすい (リンク先では更新を非同期型で行っている)。
プログラム
gist においた。
単純なデータでの確認
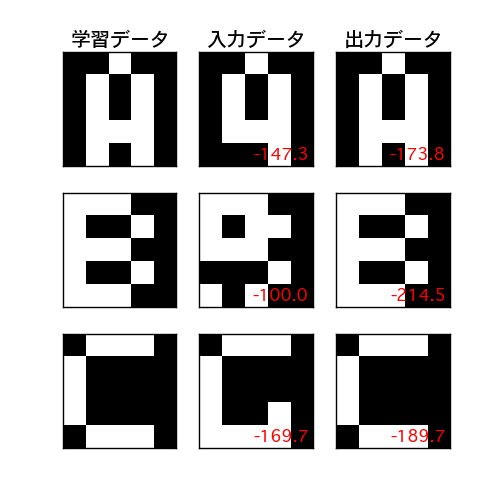
まずは 5 x 5 = 25 次元の単純な 文字データを 3 種類 用意し、動作を確認してみる。
data = [np.array([0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0]), np.array([1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0]), np.array([0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0])] data = [d * 2 - 1 for d in data] # Hopfield Network インスタンスの作成 & 学習 hn = HopfieldNetwork() hn.fit(data) # 画像に 10% のノイズを付与し、テストデータとする test = [get_corrupted_input(d, 0.1) for d in data] # Hopfield Network からの出力 predicted = hn.predict(test) plot(hn, data, test, predicted, figsize=(5, 5))
左列にある 3 つの学習データによって学習した HNN に、中央列の入力データ ( 学習データに 10% のノイズを付与したデータ )を与えた。その際の出力値は 右列 出力データに示す画像となる。HNN は 3つの学習データを記憶しており、入力されたデータに最も近い学習データを出力していることがわかる。
また、入力 / 出力それぞれの右下の数値 ( 赤字 ) がその時点でのネットワーク エネルギーになる。入力と比べ、出力のエネルギーは常に小さくなっている。
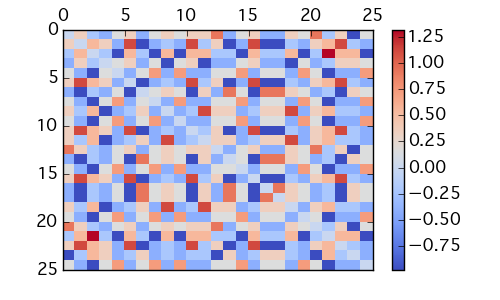
HNN の重み行列はこんな感じ。対角成分 0 の対象行列となり、相関が強い要素に対応する値が大きくなっている。
hn.plot_weight()
MNISTデータでの確認
MNIST データのうち、適当な 5 画像を選んで動作をみてみる。MNIST データは上のサンプルと比べると 白黒 2値の比率に偏りがあり、余白部分である -1 の比率が大きい。このまま HNN で処理をかけると、 余白部分の相関に影響されて特徴部分 ( 文字列部分 ) の特徴がうまくとりだせず、ネットワークの出力値がゴミになる。HNN の重み行列もこんな感じ。
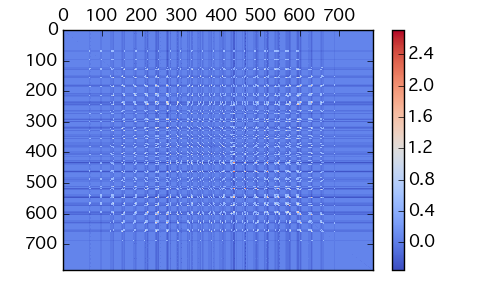
これを防ぐには適当に閾値を考慮すればよい。閾値を変化させたときの 出力値の変化をアニメーションさせてみた。
def preprocessing(input): """ 画像を2値 {-1, 1} に変換 """ input = (input >= np.max(input) / 2).astype(int) return input * 2 - 1 # MNIST データをダウンロード / ロード from sklearn.datasets import fetch_mldata mnist = fetch_mldata('MNIST original', data_home=".") # 5件 データを取得 data = mnist.data[[0, 7000, 14000, 21000, 28000, 35000]] data = [preprocessing(d) for d in data] hn = HopfieldNetwork() hn.fit(data) test = [get_corrupted_input(d, 0.1) for d in data] for i in range(0, 80): predicted = hn.predict(test, threshold=i) fig, axes = plot(hn, data, test, predicted) fig.suptitle('閾値 {0:.2f}'.format(i)) plt.savefig('mnist_bias_{0}.png'.format(i))
閾値が小さすぎると、学習データの特徴部分が全て出てくる / 閾値が大きすぎると出力がすべて -1 となり何もでてこない。今回のデータの場合 閾値がおよそ 45-50 くらいの場合 (アニメーションが一時停止するあたり) でそこそこの出力が得られた。
学習データと完全に一致する出力が得られていないのは 局所解に落ちているためと思われる。

閾値 = 何かを思い出そうとするときのハードル、と考えると 人間のアタマの動きと似ていておもしろい。
補足 閾値もエネルギー計算式に含まれるため、同じ入力値であっても 閾値が違えばエネルギーは異なる。
HNN の更新処理
最後に、上記の HNN がランダムな入力を受けたときにどのような動きをするかみる。閾値は上の値ではうまくいかなかったので適当に変えた。
fig, axes = plt.subplots(4, 3, figsize=(5, 6)) axes = axes.flatten() for i, ax in enumerate(axes): test = [get_corrupted_input(np.ones(28*28), 0.5)] predicted = hn.predict(test, threshold=30, loop=i) hn.plot_data(ax, predicted[0], with_energy=True) ax.set_title('t={0}'.format(i), size=9) ax.xaxis.set_visible(False) ax.yaxis.set_visible(False) plt.show()
HNN にランダムな入力を与えた後、更新を t 回実施した時の各ユニットの状態を画像として描画した。t が増えるほど エネルギーは減っていき、t = 9 以降は一定になっている。このとき、 HNN の出力は t = 9 のものになる。
ランダムな入力に対しても、HNN の更新を繰り返すことによって 記憶した学習データに近い状態へと変化していくことがわかる。

まとめ
- ホップフィールドネットワークを Python で実装し、その動きをみた。学習データが重み行列としてネットワーク内に記憶され、入力データへの更新処理によって学習データが復元されることがわかった。ただし、データによっては完全に復元できないこともある。
- (すごく乱暴に言うと) HNN のグラフ構造を変更 / 動作を確率的にすると 制約付きボルツマンマシンになる。以下記事のマルコフ確率場とあわせて、これで制約付きボルツマンマシンへいく準備ができた。
1/12追記 つづきはこちら。

- 作者: 岡谷貴之
- 出版社/メーカー: 講談社
- 発売日: 2015/04/08
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る