R の {MSwM} パッケージでマルコフ転換モデルをためす
マルコフ転換モデルとは
数式を使わない説明。
サーモンとインターネット広告とマルコフ転換モデル|インターネット広告代理店で働くデータサイエンティストのブログ
マルコフ状態転換モデルのRパッケージ{MSwM}の使い方(異常値検出・ステータス変化検出などに有用) - 銀座で働くData Scientistのブログ
Exampleとしては vignettes がわかりやすい。
http://cran.r-project.org/web/packages/MSwM/vignettes/examples.pdf
まず
手元には下図のような時系列データがあるとする。経験的になんとなく 目的変数 y は説明変数 x に関係していそう、ということがわかっている。が、ぱっと見でも y のレベルが途中でシフトしており、常に一定の関係がなりたっているわけではなさそう (背後に複数の状態がありそう)。
こんなときにマルコフ転換モデルを使うと 背後にある状態変化を踏まえて モデルを作ってくれる。

上のサンプルデータは以下のようにして作った。時点に応じて x, y の関係が切り替わるデータとなっている。
※説明変数は目的変数とまったく関係のないものでもよいが、(一部の状態にでも)関係していそうなものを選んだほうがよい。説明変数が目的変数と関係ないものだと 切片の変化 = ベースラインの変化でしか状態転換を検出できないと思う。その場合マルコフ転換を使う必要がない。
x <- rpois(500, lambda = 10) # x はポアソン分布に従う y1 <- x * 4 + 20 # 状態1のときの x, yの関係 y2 <- x * 2 + 60 # 状態2のときの x, yの関係 # ノイズ付与 noise <- rnorm(1:500, mean = 10, sd = 5) y1 <- y1 + noise y2 <- y2 + noise # 適当なタイミングで状態転換 (1:200までは状態1, 201:400までは状態2, 以降は状態1) y <- c(y1[1:200], y2[201:400], y1[401:500]) # 実際に観測されたデータ observed <- data.frame(x = x, y = y)
x と y1, y2の関係を図示すると下図のようになる。x, yに二つの状態があることがわかっていれば、 x, yはこのように見える。
状態別に分離したデータ

が、観測者にとっては 状態がそもそもいくつあるのかすらわかっていない。そのため x, yは 状態の区別なくひとまとまりで見える。マルコフ転換モデルでは、観測データがいくつかの状態から発生していると捉えて、うまいこと上図のように分離してくれる。
観測されるデータ

マルコフ転換モデルの作成
{MSwM} でマルコフ転換モデルを作るのは非常にカンタンで、
- 目的変数/説明変数の関係を 線形回帰モデル, もしくは一般化線形モデルとして記述する
- 1で作ったモデル式とパラメータを
MSwM::msmFitに渡してマルコフ転換モデルをフィットさせる
だけ。
モデル式作成
ここでは y と x は線形関係にあるものとして、lm 関数でモデル式を作る。この状態 (全体をひとつの状態として線形回帰した場合)で summary 表示して Coefficients をみると、ちょうど y1, y2の間くらいに線を引いていることがわかる。残差が大きいので 調整済みR二乗値も低い。
library(MSwM) m.lm <- lm(y ~ x, data = observed) summary(m.lm) # # Call: # lm(formula = y ~ x, data = observed) # # Residuals: # Min 1Q Median 3Q Max # -24.303 -9.354 -1.914 9.617 29.224 # # Coefficients: # Estimate Std. Error t value Pr(>|t|) # (Intercept) 45.7468 1.7202 26.59 <2e-16 *** # x 3.2262 0.1636 19.71 <2e-16 *** # --- # Signif. codes: # 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 11.51 on 498 degrees of freedom # Multiple R-squared: 0.4383, Adjusted R-squared: 0.4372 # F-statistic: 388.7 on 1 and 498 DF, p-value: < 2.2e-16
モデルのフィット
上で作ったモデルを msmFit に渡せばよい。パラメータの意味は、
k: マルコフ転換モデルの状態数。 ここでは 背後に2つの状態があるものとして指定。sw: 各パラメータが状態転換時に変化するかどうかを Logical で指定p: ARモデルの係数family: (GLMの場合) 確率分布の family
m.mswm <- msmFit(m.lm, k = 2, sw = c(TRUE, TRUE, TRUE, TRUE), p = 1) summary(m.mswm) # Markov Switching Model # # Call: msmFit(object = m.lm, k = 2, sw = c(TRUE, TRUE, TRUE, TRUE), # p = 1) # # AIC BIC logLik # 3038.846 3101.397 -1513.423 # # Coefficients: # # Regime 1 # --------- # Estimate Std. Error t value Pr(>|t|) # (Intercept)(S) 69.3263 4.0606 17.0729 <2e-16 *** # x(S) 2.1795 0.1187 18.3614 <2e-16 *** # y_1(S) -0.0103 0.0429 -0.2401 0.8103 # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 4.99756 # Multiple R-squared: 0.6288 # # Standardized Residuals: # Min Q1 Med Q3 Max # -1.431396e+01 -2.056292e-02 -1.536781e-03 -1.098923e-05 1.584478e+01 # # Regime 2 # --------- # Estimate Std. Error t value Pr(>|t|) # (Intercept)(S) 30.2820 1.7687 17.1210 <2e-16 *** # x(S) 3.9964 0.0913 43.7722 <2e-16 *** # y_1(S) -0.0045 0.0203 -0.2217 0.8245 # --- # Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 # # Residual standard error: 4.836684 # Multiple R-squared: 0.8663 # # Standardized Residuals: # Min Q1 Med Q3 Max # -13.202056966 -0.771854514 0.002211602 1.162769110 12.417873232 # # Transition probabilities: # Regime 1 Regime 2 # Regime 1 0.994973376 0.003347279 # Regime 2 0.005026624 0.996652721
出力中の Regime 1, Regime 2が 背後にある(と考えられる)二つの状態をあらわす。y の真の値と比較すると、出力中の Regime 1が y2 <- x * 2 + 60 に対応しており、
# Regime 1 # --------- # Estimate Std. Error t value Pr(>|t|) # (Intercept)(S) 69.3263 4.0606 17.0729 <2e-16 *** # x(S) 2.1795 0.1187 18.3614 <2e-16 *** # y_1(S) -0.0103 0.0429 -0.2401 0.8103
Regime 2が y1 <- x * 4 + 20 と対応していることがわかる。
切片のずれが少し気になるがノイズのせいかな、、?調整済みR二乗値から全体として改善しているとは言える。
# Regime 2 # --------- # Estimate Std. Error t value Pr(>|t|) # (Intercept)(S) 30.2820 1.7687 17.1210 <2e-16 *** # x(S) 3.9964 0.0913 43.7722 <2e-16 *** # y_1(S) -0.0045 0.0203 -0.2217 0.8245
モデルのプロット
状態 (Regime) ごとに 目的変数 + 指定した説明変数と、その状態にある確率を陰影でプロット
plotReg(m.mswm, c('x'), regime = 1)

各時点がそれぞれどちらの状態 (Regime)にあるかを確率でプロット
plotProb(m.mswm, which = 1)
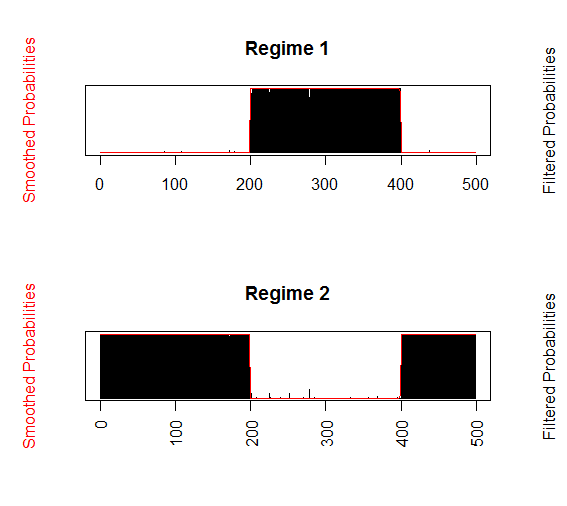
各時点の状態と変化点を取得
ある時点でどちらの状態 (Regime) にいるかを知りたい場合は、その時点で一番 発生している(していた)確率の高い Regimeを拾ってくればよい。
probable <- apply(m.mswm@Fit@smoProb[-1, ], 1, which.max) > probable [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [30] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ...
異常値 / 変化点は Regime が転換した時点になるので、上で取得したベクトルの値が変化した箇所が TRUE になるようにすると、
c(FALSE, diff(probable) != 0) [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [11] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE ... [181] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [191] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE [201] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE ... [381] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [391] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE [401] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE ... [491] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
ということで 最初のデータ作成時に指定した変化点 (201, 401番目)に近いところが検知できているのがわかる。